hugo/content/posts/leetcode.md

title	author	date	categories	tags	draft
leetcode everyday	Logic	2024-02-27			false

day 1 2024-02-27

543 Diameter of Binary Tree

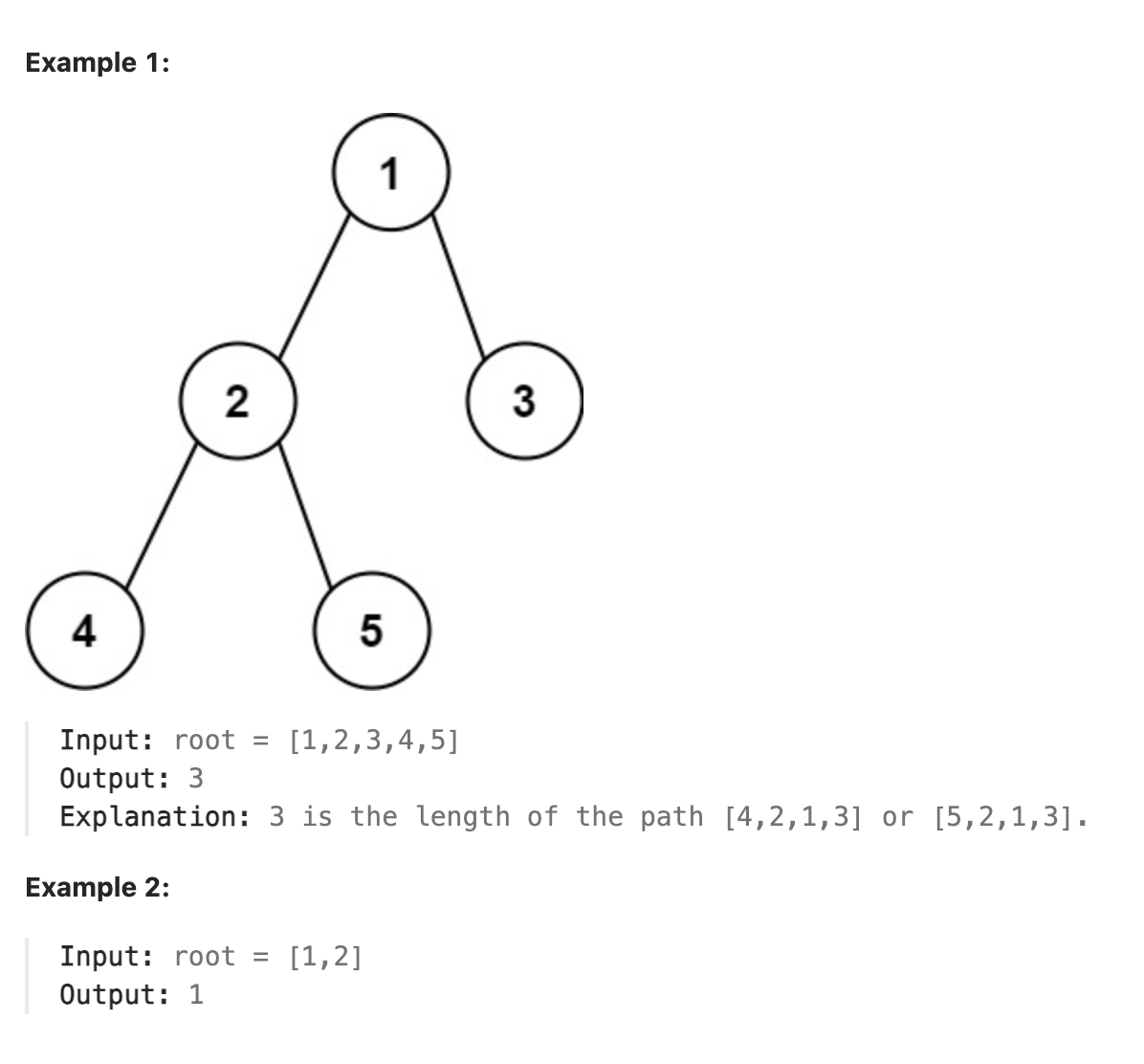
Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

题解

读题, 题目要求寻找二叉树中任意两节点之间的最大距离. 这时这个二叉树更像是一个图的性质而不是树, 即寻找图中任意两节点之间的最大距离. 考虑任意一点到另一点的距离等于其到另一点的父节点的距离减一, 则使用一个二维数组保存每个节点的两个属性:

1. 以该节点为根节点且经过该节点的最大直径
2. 以该节点为根节点的子树中叶子节点到该节点的最大距离

属性1可以通过将该节点的两个子节点的属性2加和并加1来计算. 属性2取两个子节点属性2的最大值并加1来计算. 最后遍历数组求得数组中属性1的最大值即可. 有一点动态规划的思想.

题目中并没有提供二叉树的节点总数, 则可以使用动态创建的方法, 在遍历过程中每遇到新节点就在二维数组中增加一项. 这里使用递归来对树进行后序遍历, 对空节点, 设置其属性2的值为-1, 这样保证叶子节点的属性2的值为0.

解题时遇到一个小bug, 使用了一个全局切片(数组)来保存变量时, 第一个测试用例的数据会保留到测试第二个测试用例的过程中, 这大概是因为leetcode的测试是对每个用例直接调用给出的解题入口函数, 因此需要在解题函数中将使用的全局变量初始化一下, 将数组设置为空后问题得到解决.

代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

var length [][]int

func diameterOfBinaryTree(root *TreeNode) int {
    length = nil
    _ = postorder(root)
    max := -1
    for _, value := range length{
        if value[0] > max{
            max = value[0]
        }
    }
    return max
}

func postorder(father *TreeNode) int {
    if father != nil{
        len1 := postorder(father.Left)
        len2 := postorder(father.Right)
        len := make([]int,2)
        // find the max diameter pass through current node from the tree rooted current node
        len[0] = len1 + len2 + 2
        len[1] = max(len1, len2) + 1
        length = append(length, len)
        return len[1]
    } else {
        return -1
    }
}

day2 2024-02-28

513. Find Bottom Left Tree Value

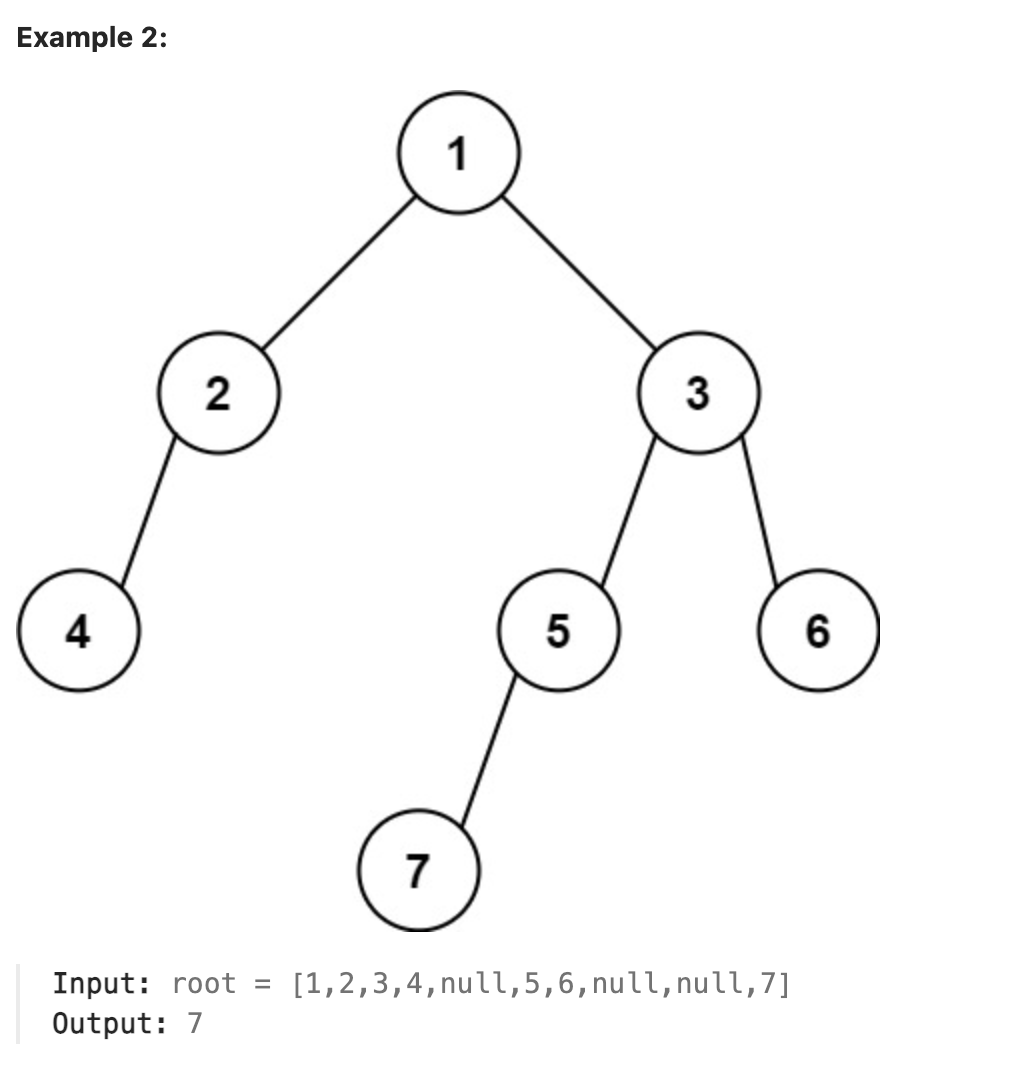
Given the root of a binary tree, return the leftmost value in the last row of the tree.

题解

找到二叉树最底层最左边的节点值, 用层序遍历遍历到最后一层找到最后一层最左边节点的值即可. 实现层序遍历可以使用一个队列, 将当前层节点的所有子节点入队后将当前层节点出队. 在go中可以使用切片实现一个队列. 使用一个标记变量记录当前层所有节点是否有子节点, 若无子节点则当前层为最低层, 返回当前层最左侧节点的值(此时队列中第一个节点的值).

代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func findBottomLeftValue(root *TreeNode) int {
    queue := []*TreeNode{root}
    lowest := false
    key := -1
    var father *TreeNode
    for !lowest{
        queue = queue[key+1:]
        lowest = true
        for key, father = range queue{
            if(father.Left != nil || father.Right != nil){
                lowest = false
                if(father.Left != nil){
                    queue = append(queue, father.Left)
                }
                if(father.Right != nil){
                    queue = append(queue, father.Right)
                }
            }
        }

    }
    return queue[0].Val
}

总结

在题解中看到了一个使用深度优先搜索的方法, 记录当前搜索到的层级, 始终保存最大层级的第一个被搜索到的值, 因为使用的是后序遍历, 则每次遇到的当前层大于保存的最大层级时, 该节点就为新的最大层级的第一个节点, 即题目中要求的最左值(leftmost). 算法时间复杂度为O(n)------只遍历一次所有节点.

day3 2024-02-29

1609. Even Odd Tree

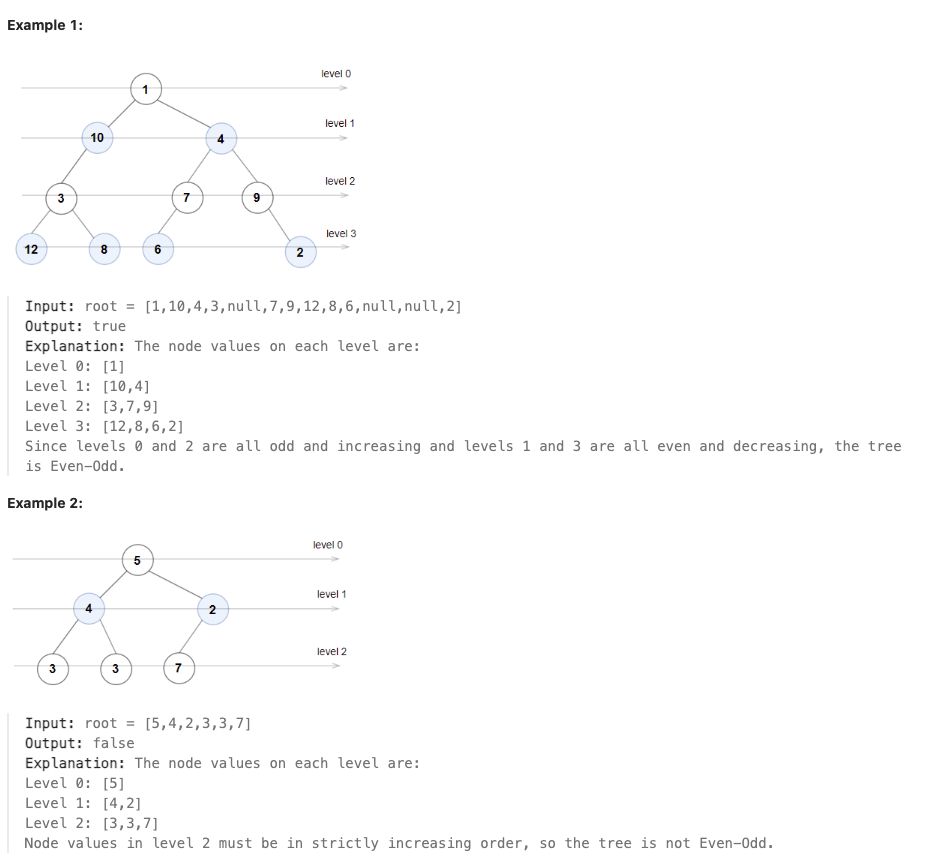
A binary tree is named Even-Odd if it meets the following conditions:

The root of the binary tree is at level index 0, its children are at level index 1, their children are at level index 2, etc. For every even-indexed level, all nodes at the level have odd integer values in strictly increasing order (from left to right). For every odd-indexed level, all nodes at the level have even integer values in strictly decreasing order (from left to right). Given the root of a binary tree, return true if the binary tree is Even-Odd, otherwise return false.

题解

对二叉树的奇数层, 其节点从左到右是严格递减的(意味着有两个节点的值相同是不允许的), 偶数层是严格递增的. 仍然可以使用昨天题目的层序遍历的方法, 增加一个level变量记录当前层数, 对该层内的节点值进行判断是否符合奇数层和偶数层对应的条件即可.

代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isEvenOddTree(root *TreeNode) bool {
    level := 0
    index := -1
    var value *TreeNode
    queue := []*TreeNode{root}
    saved := 0
    for len(queue) != 0{
        // remove visited nodes
        queue = queue[index+1:]
        index = 0
        if(level%2 == 0){
            for index, value = range queue{
                if(index == 0){
                    saved = value.Val
                    if(saved %2 != 1){return false}
                } else{
                    if(value.Val <= saved || (value.Val%2) != 1){
                        return false
                    } else{
                        saved = value.Val
                    }
                }
                if(value.Left != nil){queue = append(queue, value.Left)}
                if(value.Right != nil){queue = append(queue, value.Right)}
            }
            level++
        } else{
            for index, value = range queue{
                if(index == 0){
                    saved = value.Val
                    if(saved %2 != 0){return false}
                } else{
                    if(value.Val >= saved || value.Val %2 != 0){
                        return false
                    } else{
                        saved = value.Val
                    }
                }
                if(value.Left != nil){queue = append(queue, value.Left)}
                if(value.Right != nil){queue = append(queue, value.Right)}
            }
            level++
        }
    }
    return true
}

总结

go语言中的for range循环, 如果使用类似for key, value := range list 的形式, 那么key, value这两个变量都会在当前作用域下新建, 意味着即使在前面定义了key, key的值在循环结束后也不会被修改. 若想修改之前定义的key值, 需要将value也提前定义好并使用=而不是:=.

go语言中的for range循环时如果使用:=会新建两个变量, 然后将slice中的值复制给value变量, 将对应的index值赋值给key变量, 这意味着value变量不会指向数组中对应位置的地址, 而是一个不变的单独地址.