Logic/hugo
1
0
Fork 0
mirror of https://gitlab.com/game-loader/hugo.git synced 2025-04-20 05:52:07 +08:00
Code Issues Actions Packages Projects Releases Wiki Activity

leetcode update

Browse Source
This commit is contained in:
gameloader 2024-04-25 15:39:23 +08:00
parent b004b3bfc7
commit 2c612d3633
1 changed files with 229 additions and 0 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

229
content/posts/leetcode.md
View File

@ -4192,3 +4192,232 @@ func findMinHeightTrees(n int, edges [][]int) []int {
return queue
}
```
## day57 2024-04-24
### 1137. N-th Tribonacci Number
The Tribonacci sequence Tn is defined as follows:
T0 = 0, T1 = 1, T2 = 1, and Tn+3 = Tn + Tn+1 + Tn+2 for n >= 0.
Given n, return the value of Tn.
![0424W6tl0Lo6n0pg](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0424W6tl0Lo6n0pg.png)
### 题解
一个简单的动态规划即可.
### 代码
```go
func tribonacci(n int) int {
if n == 0{
return 0
}else if n == 1{
return 1
}else if n == 2{
return 1
}else{
arrays := []int32{0,1,1}
var result int32
for i:=3;i<=n;i++{
result = arrays[i-1]+arrays[i-2]+arrays[i-3]
arrays = append(arrays, result)
}
return int(result)
}
}
```
今天题目有些过于简单了,遂再补一道题
### 2385. Amount of Time for Binary Tree to Be Infected
You are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.
Each minute, a node becomes infected if:
The node is currently uninfected.
The node is adjacent to an infected node.
Return the number of minutes needed for the entire tree to be infected.
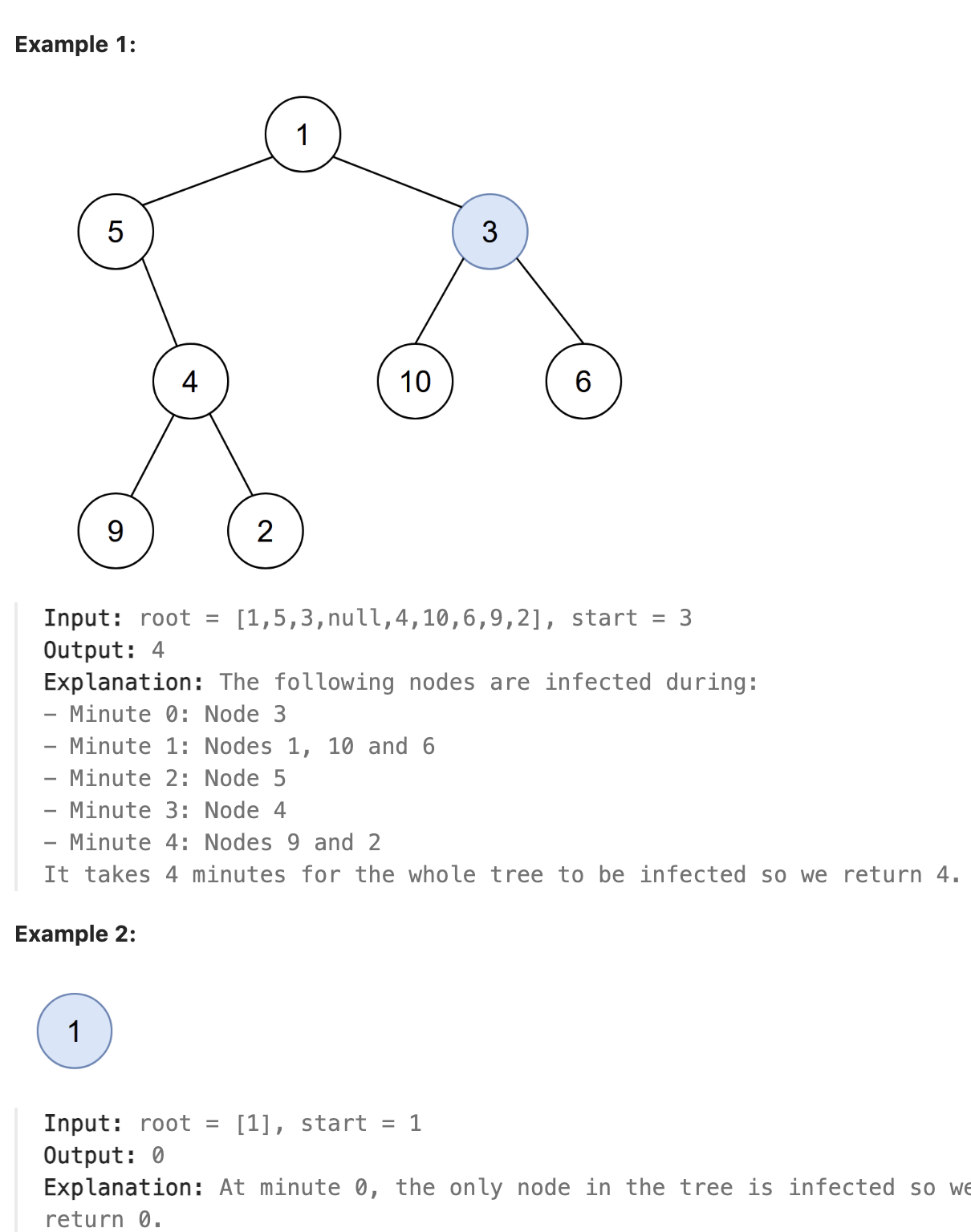
![0424X5IWeZmiTuqj](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0424X5IWeZmiTuqj.png)
### 题解
这道题第一眼看上去就像在一个图中给定一个节点,寻找这个图中与这个节点距离最远的节点的距离.然而题面条件是二叉树,因此最直观的方法就是将二叉树转换为无向图, 再使用BFS找到最远的距离, 这样需要将所有节点遍历两遍.
### 代码
```go
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func amountOfTime(root *TreeNode, start int) int {
undirected_map := map[int][]int{}
undirected_map[root.Val] = []int{}
queue := []*TreeNode{root}
for len(queue) != 0{
for _, node := range queue{
if node.Left != nil{
undirected_map[node.Val] = append(undirected_map[node.Val],node.Left.Val)
undirected_map[node.Left.Val] = []int{node.Val}
queue = append(queue, node.Left)
}
if node.Right != nil{
undirected_map[node.Val] = append(undirected_map[node.Val],node.Right.Val)
undirected_map[node.Right.Val] = []int{node.Val}
queue = append(queue, node.Right)
}
queue = queue[1:]
}
}
visited := make([]int,100001)
neibor := []int{start}
visited[start] = 1
time := 0
for len(neibor) != 0{
for _,node := range neibor{
for _,value := range undirected_map[node]{
if visited[value] != 1{
neibor = append(neibor, value)
visited[value] = 1
}
}
neibor = neibor[1:]
}
time++
}
return time-1
}
```
### 总结
显然这种方法略慢, 要是可以在一次遍历的时候保存一定的信息, 减少重复的节点访问就好了, 思考这棵二叉树, 如果我们知道了从根节点到开始节点的距离, 并且保存了从根节点到开始节点的路径, 那么最远距离分为两种情况, 要么是以开始节点为根节点的子树足够深, 要么是开始节点的祖先节点的另外一棵子树足够深, 二者哪个更大就取哪个的最远距离. 尽管思路如此, 但当时我的想法是这样在寻找从根节点到开始节点时也要使用DFS, 这样在最差情况也要访问整棵树, 但实际上平均情况下会少访问大概以开始节点为根节点的子树的节点. 这样当节点数很多的时候也有一定的复杂度优势. 但是事实证明, 我想的还是不够全面, 实际上我们在递归调用的时候可以通过返回更多信息(一个布尔值)来标记该节点的某个子树上含有开始节点, 同时返回当前节点距离开始节点的距离. 这样通过一个非常巧妙的信息流动, 在开始节点处判断了以开始节点为根节点的子树的最大深度, 从开始节点处递归返回时向祖先节点传递该子树包含开始节点和距离开始节点的距离信息. 这样充分利用了在递归遍历过程中的全部信息. 只需要一次遍历即可解决. 充分的利用和整合信息是提高算法效率的关键, 示例代码如下
```go
func amountOfTime(root *TreeNode, start int) int {
if root == nil {
return 0
}
r := 0
//
// returns true if start is a child of p.
// and the distance from this node to start.
// false if the start is not child of p.
// and the longest distance to a leave in this subtree.
//
var dfs func(p * TreeNode) (bool, int)
dfs = func(p * TreeNode) (bool, int) {
ll, rr, lh, rh := 0, 0, false, false
if p.Left != nil {
lh, ll = dfs(p.Left)
ll++
}
if p.Right != nil {
rh, rr = dfs(p.Right)
rr++
}
if p.Val == start {
if r < ll {
r = ll
}
if r < rr {
r = rr
}
return true, 0 // 0 to get the dist to parent
}
if lh {
if ll + rr > r {
r = ll + rr
}
return true, ll
}
if rh {
if ll + rr > r {
r = ll + rr
}
return true, rr
}
if ll < rr {
ll = rr
}
return false, ll
}
dfs(root)
return r
}
```
## day58 2024-04-25
### 2370. Longest Ideal Subsequence
You are given a string s consisting of lowercase letters and an integer k. We call a string t ideal if the following conditions are satisfied:
t is a subsequence of the string s.
The absolute difference in the alphabet order of every two adjacent letters in t is less than or equal to k.
Return the length of the longest ideal string.
A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
Note that the alphabet order is not cyclic. For example, the absolute difference in the alphabet order of 'a' and 'z' is 25, not 1.
![0425VwyUwgCD4hKc](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0425VwyUwgCD4hKc.png)
### 题解
字符串子序列问题是一类很经典的递推计数问题. 一般可以用动态规划来解决. 问题的关键在于如何找到问题的子问题. 对于本题, 思考通过贪心等方式直接找到最长的子序列显然是不可行的, 因为一个字符在当前串中作为结尾可以使该串长度增大, 但后续可能有更长的串与没有这个字符的串可以连接, 但加上这个字符使得这个更长的串不能连接了. 显然考虑的不够周全. 那么现在还是要紧紧围绕我们在解题时多次提到过的思想: 能更有效的利用更多的信息, 算法的效率就越高. 对于一个字符来说, 哪些信息是有用的, 与之相差k个距离以内的字符是有用的, 因为这些字符可以与当前字符连接. 用贪心难以解决的原因在于, 只考虑了和当前字符相邻的k以内这一群邻居中的一个, 自然不能高效求解. 那么我们只要一直保存着所有以字符结尾的子序列的长度, 在遇到新字符时只需要对k个距离内的字符子序列进行比较, 找出最长的并将其加1作为当前字符的最长子序列长度. 这样充分利用了以前遍历过的可行字符组合的信息. 并将所有邻居都考虑进来, 最终就能得到可行解.
### 代码
```go
func longestIdealString(s string, k int) int {
lengths := make([]int32, 26)
var left int32
var right int32
var temp_max int32
k32 := int32(k)
for _,value := range s{
temp_max = 0
left = value - 'a' - k32
right = value - 'a' + k32
if value - 'a' < k32{
left = 0
}
if 'z' - value < k32{
right = 25
}
for _, number := range lengths[left:right+1]{
temp_max = max(number, temp_max)
}
lengths[value - 'a'] = temp_max + 1
}
return int(slices.Max(lengths))
}
```