leetcode update

content/posts/leetcode.md

@@ -4059,3 +4059,136 @@ func openLock(deadends []string, target string) int {
 ### 总结
 
 遇到题面看上去复杂的题目需要将题目的核心问题抽离出来. 若题目本身解决起来比较困难, 可以先尝试思考解决题目的一个子问题, 如降低维度, 减少数量, 再尝试推广到题目本身. 另外在数学中往往从一维到二维有很多不同点, 可能需要全新的工具和解决方式. 但从二维到更高维往往只是简单推广, 这也是为什么很多数学问题只证明二维的情况即可代表全部高维情况的原因.
+
+## day56 2024-04-23
+
+### 310. Minimum Height Trees
+
+A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.
+
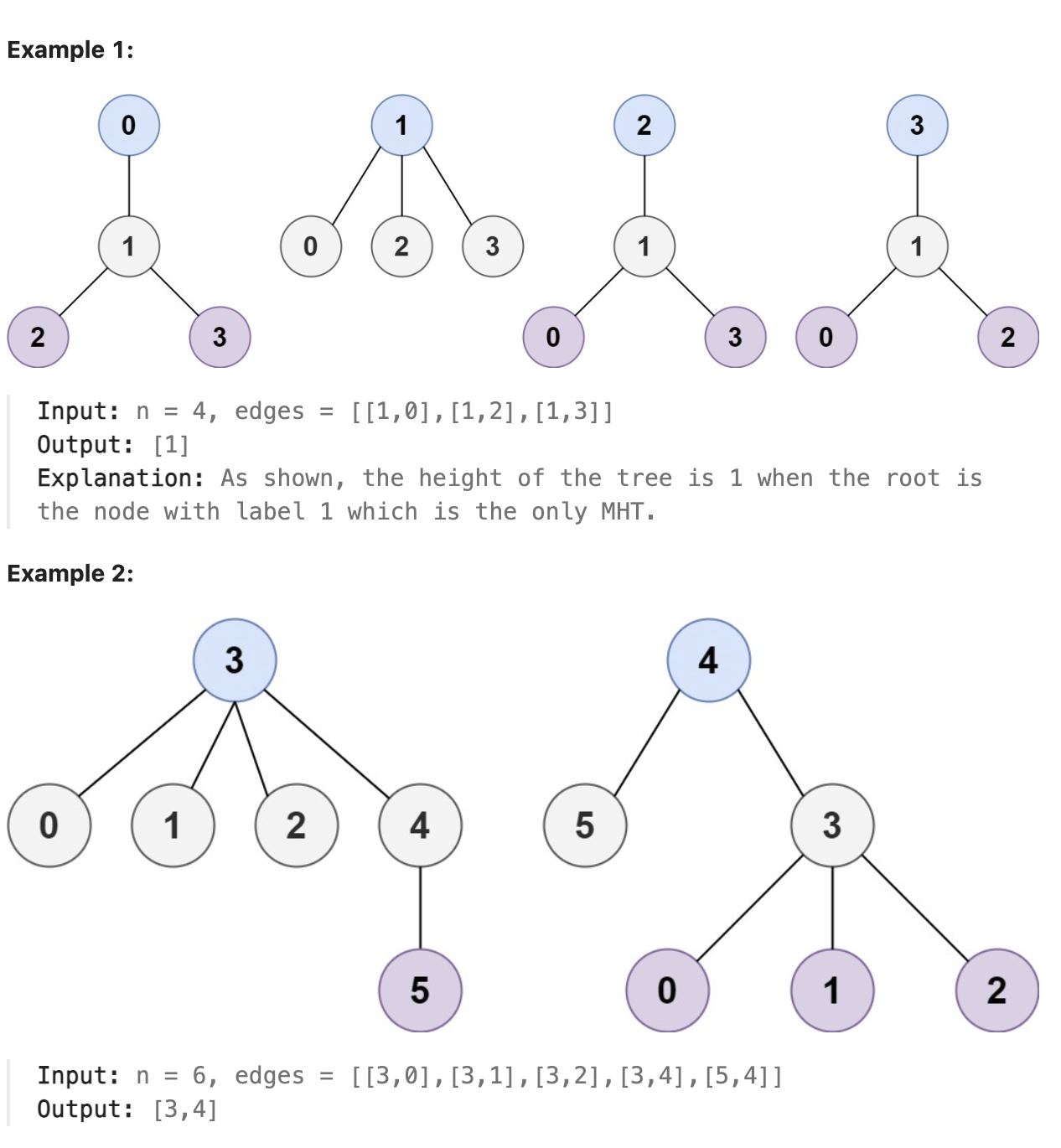
+Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).
+
+Return a list of all MHTs' root labels. You can return the answer in any order.
+
+The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
+
+![0423RbJZu7RPqeXz](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0423RbJZu7RPqeXz.png)
+
+### 题解
+
+本题乍一看让人摸不着头脑, 细细想想最远的距离肯定是从一个叶子节点到另一个叶子节点, 那么最小高度的子树就是位于这个最远路径上中间位置的一个或者两个节点(取决于路径的长度是奇数还是偶数). 则本题的关键在于求出该无向图中的最长路径, 求出无向图中最长路径可以选择任一叶子节点, 对其进行dfs, 再将得到的当前最长路径的终点作为起点, 进行dfs即可得到全图的最长路径.
+
+### 代码
+
+```go
+func findMinHeightTrees(n int, edges [][]int) []int {
+    if n == 1{
+        return []int{0}
+    }
+    numbers := map[int]int{}
+    graph := map[int][]int{}
+    exist := false
+    for _,value := range edges{
+        for index,vertex := range value{
+            _, exist = numbers[vertex]
+            if !exist{
+                numbers[vertex] = 1
+                graph[vertex] = []int{value[1-index]}
+            }else{
+                numbers[vertex]++
+                graph[vertex] = append(graph[vertex], value[1-index])
+            }
+        }
+    }
+    start := 0
+    for node, count := range numbers{
+        if count == 1{
+            start = node
+            break
+        }
+    }
+
+    path := []int{start}
+    depth := 1
+    path = append(path, dfs(graph[start][0], start, depth+1, graph)...)
+    length := len(path)
+    start = path[length-1]
+    depth = 1
+    newtest := []int{start}
+    newtest = append(newtest, dfs(graph[start][0], start, depth+1,graph)...)
+    if len(newtest) > length{
+        path = newtest
+        length = len(newtest)
+    }
+    if length % 2 == 1{
+        return []int{path[length/2]}
+    }else{
+        return []int{path[length/2-1],path[length/2]}
+    }
+
+}
+
+func dfs(node int, parent int,  depth int, graph map[int][]int)[]int{
+    max := depth
+    return_path := []int{node}
+    for _,value := range graph[node]{
+        if value != parent{
+            temppath := dfs(value, node, depth+1, graph)
+            if len(temppath) + depth > max{
+                max = len(temppath) + depth
+                return_path = append(return_path[0:1], temppath...)
+            }
+        }
+    }
+    return return_path
+}
+```
+
+## 总结
+
+显然, 这种解法是相当慢的, 执行两次dfs也有大量的重复计算. 这里解决本题可以使用对无向图的拓扑排序. 排序操作为设定一个队列, 找到当前图中所有度为1的点, 将其删去(从队列中弹出)并删去其邻接的边, 将与其相邻的点中度为1 的点放入队列. 如此重复, 直到队列中只有一个或者两个点, 即为整个图中的最长路径的中间点. 这里要理解拓扑排序其实是对图的从边缘到中心的一种刻画. 也就是对依赖关系的刻画. 越靠近"中心"的点依赖越多. 排序过程中越靠前的点离图的"中心"越远. 依赖越少. 代码如下, 很简洁
+
+```go
+func findMinHeightTrees(n int, edges [][]int) []int {
+    if n == 1 {
+        return []int{ 0 }
+    }
+
+
+    //graph := make(map[int][]int)
+    neibors := make([][]int, n)  //neibors[i]  -- all nodes node i can connect to
+    degree := make([]int, n)    //degree[i]  -- connections from node i
+
+    for _, e := range edges {
+        na, nb := e[0], e[1]
+        neibors[na] = append(neibors[na], nb)
+        neibors[nb] = append(neibors[nb], na)
+        degree[na]++
+        degree[nb]++
+    }
+   queue := []int{}
+    for i, d := range degree {
+        if d == 1 {
+            queue = append(queue, i)
+        }
+    }
+
+    // topological sort
+    for n > 2 {
+        size := len(queue)
+        n -= size
+        for i:=0;i<size;i++{
+            cur:=queue[i]
+            for _, next:=range neibors[cur]{
+                degree[next]--
+                if degree[next]==1{
+                    queue=append(queue, next)
+                }
+            }
+        }
+        queue=queue[size:]
+    }
+
+    return queue
+}
+```