mirror of
https://gitlab.com/game-loader/hugo.git
synced 2026-02-28 12:05:12 +08:00
leetcode update
This commit is contained in:
@@ -3137,3 +3137,266 @@ func deckRevealedIncreasing(deck []int) []int {
|
||||
### 总结
|
||||
|
||||
这样虽然写起来方便, 但实际上在不断append的过程中position会占用更多的空间, 使用循环队列可以避免空间的浪费.
|
||||
|
||||
## day44 2024-04-11
|
||||
|
||||
### 402. Remove K Digits
|
||||
|
||||
Given string num representing a non-negative integer num, and an integer k, return the smallest possible integer after removing k digits from num.
|
||||
|
||||

|
||||
|
||||
### 题解
|
||||
|
||||
本题考虑数字中的某一位数字能产生的影响, 对应这个数字相邻的左右两个数字, 如果删掉了相邻的数字没有删掉当前这一位的数字, 在删除后的字符串中相当于用当前这一位数字代替了被删掉的相邻数字, 如果删掉了当前的数字没删掉相邻的数字, 同样相当于在这一位上用相邻的数字代替了被删掉的数字. 即在删除后的字符串中的这一位上用当前这一位的数字和相邻数字二选一, 前后的其余字符串不用考虑不影响这个局部变化. 仅考虑这个局部变化的过程, 最优解为在删除完毕的字符串中的当前位置应该放入较小的数字, 即相邻数字中较大的数应该被删去, 考虑左右相邻的对称性, 则可以得出, 删掉比左右相邻数字都大的数可以在删掉一个数后得到局部最优解, 删掉这个数后要回溯一位判断删除后之前的数是否符合条件. 重复此过程遍历数组, 删掉k个数后返回最终的字符串.
|
||||
|
||||
### 代码
|
||||
|
||||
```go
|
||||
func removeKdigits(num string, k int) string {
|
||||
if len(num) == k{
|
||||
return "0"
|
||||
}
|
||||
index := 0
|
||||
delete := 0
|
||||
for index < len(num) && delete < k{
|
||||
if delete == 554{
|
||||
fmt.Println(num)
|
||||
}
|
||||
if index == 0{
|
||||
if len(num) == 1{
|
||||
break
|
||||
}
|
||||
if num[index] == '0'{
|
||||
num = num[1:]
|
||||
index--
|
||||
}else if num[index] > num[index+1]{
|
||||
delete++
|
||||
num = num[1:]
|
||||
index--
|
||||
}
|
||||
index++
|
||||
}else if index == len(num) - 1{
|
||||
if num[index] >= num[index-1]{
|
||||
num = num[0:len(num)-1]
|
||||
index--
|
||||
delete++
|
||||
}
|
||||
}else{
|
||||
if num[index] > num[index-1]&&num[index] >= num[index+1] || num[index] > num[index+1] && num[index] >= num[index-1]{
|
||||
num = num[0:index] + num[index+1:]
|
||||
index--
|
||||
delete++
|
||||
}else{
|
||||
index++
|
||||
}
|
||||
}
|
||||
}
|
||||
if delete < k{
|
||||
return "0"
|
||||
}
|
||||
for index = 0;num[index] == '0'&&index < len(num)-1;index++{}
|
||||
return num[index:]
|
||||
}
|
||||
```
|
||||
|
||||
### 总结
|
||||
|
||||
本题自己想出的解法效率实在不太行, 思路上也不够简洁优美, 看了前面的题解, 发现从原来的思考的基础上应该进一步思考, 对于一串数字字符串来说, 可以删除的数字数量是有限的, 则要首先让数字的高位部分尽可能小, 删除的时候不能改变未删除的数字的相对位置, 根据之前的局部最优解的思考, 如果当前位置的数字比后一位大, 则应将这一位删掉, 让后一位占据当前位置, 这样保证了当前的数字一定比后一位数字小, 这样就做到了尽可能让小的数字位于前面, 使得每一步操作结束后的子数组具有单调性. 这也意味着之前考虑前后两个相邻数字的大小是多余的, 考虑后一位即可, 只需要使用一个单调栈来保证栈末尾的数比要入栈的数字小即可. 注意处理前导0和遍历一次字符串后没有删够元素的情况即可. 代码如下
|
||||
|
||||
```go
|
||||
func removeKdigits(num string, k int) string {
|
||||
result := []rune{}
|
||||
|
||||
for _, c := range num {
|
||||
for len(result) > 0 && result[len(result) - 1] > c && k > 0 {
|
||||
result = result[:len(result) - 1]
|
||||
k--
|
||||
}
|
||||
if len(result) > 0 || c != '0' {
|
||||
result = append(result, c)
|
||||
}
|
||||
}
|
||||
|
||||
for len(result) > 0 && k > 0 {
|
||||
result = result[:len(result) - 1]
|
||||
k--
|
||||
}
|
||||
|
||||
if len(result) <= 0 {
|
||||
return "0"
|
||||
}
|
||||
return string(result)
|
||||
}
|
||||
```
|
||||
|
||||
## day45 2024-04-12
|
||||
|
||||
### 42. Trapping Rain Water
|
||||
|
||||
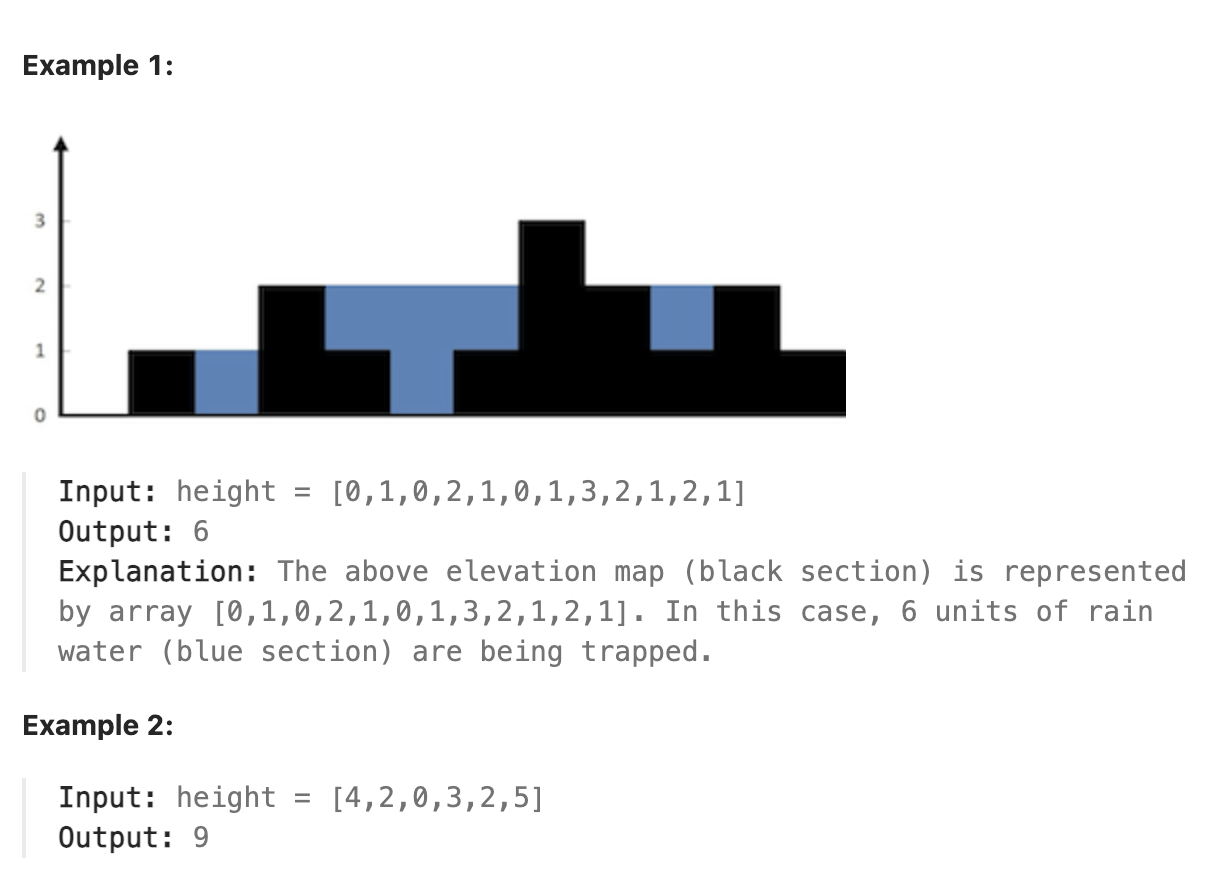
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.
|
||||
|
||||
|
||||
|
||||
### 题解
|
||||
|
||||
本题是leetcode中一道经典难题, 思路上和昨天的题目有一些相似, 仍然思考局部的情况, 对于任一位置而言, 其在竖直方向上能接到的水的单位数与其自身的高度和其两侧的最高的"墙"的高度有关. 因此关键在于求出任一位置的两侧高度最高的"墙"的高度有多高. 可以使用两个数组来保存某一位置前面的最高的墙的高度和后面的最高墙的高度. 求最高墙的高度的过程可以通过动态规划解决, 用一个数记录当前位置左侧的最高墙高度是多少, 与自身比较, 如果该位置更高, 则更新最高高度, 否则将当前位置的左侧最高墙高度设置为之前的最高墙高度. 对于右侧同理.
|
||||
|
||||
### 代码
|
||||
|
||||
```go
|
||||
func trap(height []int) int {
|
||||
highest := 0
|
||||
left_high := []int{}
|
||||
right_high := make([]int,len(height))
|
||||
for _,value := range height{
|
||||
if value > highest{
|
||||
highest = value
|
||||
}
|
||||
left_high = append(left_high, highest)
|
||||
}
|
||||
highest = 0
|
||||
for i:=len(height)-1;i>=0;i--{
|
||||
if height[i] > highest{
|
||||
highest = height[i]
|
||||
}
|
||||
right_high[i] = highest
|
||||
}
|
||||
result := 0
|
||||
for index,value := range height{
|
||||
result += min(left_high[index],right_high[index]) - value
|
||||
}
|
||||
return result
|
||||
}
|
||||
```
|
||||
|
||||
### 总结
|
||||
|
||||
看题解时发现一种更巧妙高效的思路, 之前提到对每一个位置能接的雨水仅与其左右的最高墙高度有关, 那么可以把同时需要知道两个方向的信息固定为只需要考虑一个方向的信息即可. 如果当前位置右侧有墙比当前位置左侧所有墙都高, 那么只需要考虑当前位置左侧最高的墙有多高就可以计算出能接的雨水, 直到出现了墙比右侧的最高的墙还高, 此时就移动尾部的指向右侧最高墙的指针, 向左移动, 此时已知左侧的最高墙比目前尾部指针右侧的所有墙都高, 因此同样只需考虑右侧最高的墙有多高即可, 直到出现墙比左侧的最高墙高, 则再次交换主导权, 移动头部方向的指针. 如此轮换移动指针, 将需要同时比较两个方向的问题简化成了只需要比较一个方向的问题, 保留了更多的信息, 只需要遍历一遍数组即可求得结果.
|
||||
|
||||
```go
|
||||
func trap(height []int) int {
|
||||
left, right := 0, len(height) - 1
|
||||
leftWall, rightWall := 0,0
|
||||
ans:=0
|
||||
for left < right {
|
||||
if height[left] < height[right] {
|
||||
leftWall = max(height[left], leftWall)
|
||||
ans += leftWall - height[left]
|
||||
left++
|
||||
} else {
|
||||
rightWall = max(height[right], rightWall)
|
||||
ans += rightWall - height[right]
|
||||
right--
|
||||
}
|
||||
}
|
||||
return ans
|
||||
}
|
||||
```
|
||||
|
||||
## day46 2024-04-13
|
||||
|
||||
### 85. Maximal Rectangle
|
||||
|
||||
Given a rows x cols binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.
|
||||
|
||||

|
||||
|
||||
### 题解
|
||||
|
||||
本题可以在一层层遍历矩阵的过程中, 将每一行中每个位置的元素按照如下规则进行操作加入到当前的列状态数组中. 若值为1且之前的列状态值大于0, 则增加对应的列状态值. 若值为0则用0替换对应的列状态值, 这样相当于在列状态中保存了从以该行为底该列中向上连续为1的值的个数. 根据当前的列状态即可求得到当前行为止以当前行为底的全为1的矩形区域中1的数量(仅包含1的矩形区域的面积). 如此不断遍历每一行并执行操作, 计算以该行为底的区域面积, 并更新面积最大值. 最后返回结果即可.
|
||||
要解决的第二个问题就是如何求得以该行为底的最大矩形区域面积, 可以使用单调栈来保存之前的列的值, 如果遇到了比栈顶值小的列, 则将之前的最大列占据的面积求出来, 直到当前列值比栈顶大为止. 这里关键在于若后面的列值比前面某一个都大, 则前面的那一列的值可以一直扩展到后面, 在求面积时即用前面某一列的值乘以所有大于等于其值的连续的列的数量(即矩形的宽度)即可得到该列对应的得到的矩形面积. 而遇到更小的列时说明前面的某些列不能继续扩展了, 就要求出之前得到的面积是多少. 这里想起来有一些复杂, 可以细细思考一下.
|
||||
|
||||
### 代码
|
||||
|
||||
```go
|
||||
func maximalRectangle(matrix [][]byte) int {
|
||||
now := make([]int, len(matrix[0]))
|
||||
maxarea := 0
|
||||
for _, row := range matrix{
|
||||
for index, number := range row{
|
||||
if number == '1'{
|
||||
now[index] += 1
|
||||
}else{
|
||||
now[index] = 0
|
||||
}
|
||||
}
|
||||
stack := []int{0}
|
||||
maxarea = max(maxarea,now[0])
|
||||
for index, value := range now[1:]{
|
||||
for len(stack)>0 && now[stack[len(stack)-1]] > value{
|
||||
length := len(stack)
|
||||
prev := now[stack[length-1]]
|
||||
stack = stack[:len(stack)-1]
|
||||
width := index + 1
|
||||
if len(stack) > 0{
|
||||
width = index - stack[length-2]
|
||||
}
|
||||
maxarea = max(maxarea, width*prev)
|
||||
}
|
||||
if len(stack) > 0 && value == now[stack[len(stack)-1]]{
|
||||
stack[len(stack)-1] = index+1
|
||||
continue
|
||||
}else{
|
||||
stack = append(stack, index+1)
|
||||
}
|
||||
}
|
||||
length := len(now)
|
||||
for len(stack) > 0 && now[stack[len(stack)-1]] != 0{
|
||||
width := length
|
||||
prev := now[stack[len(stack)-1]]
|
||||
stack = stack[:len(stack)-1]
|
||||
if len(stack) > 0{
|
||||
width = length - stack[len(stack)-1] - 1
|
||||
}
|
||||
maxarea = max(maxarea,width*prev)
|
||||
}
|
||||
}
|
||||
return maxarea
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
## day47 2024-04-14
|
||||
|
||||
### 404. Sum of Left Leaves
|
||||
|
||||
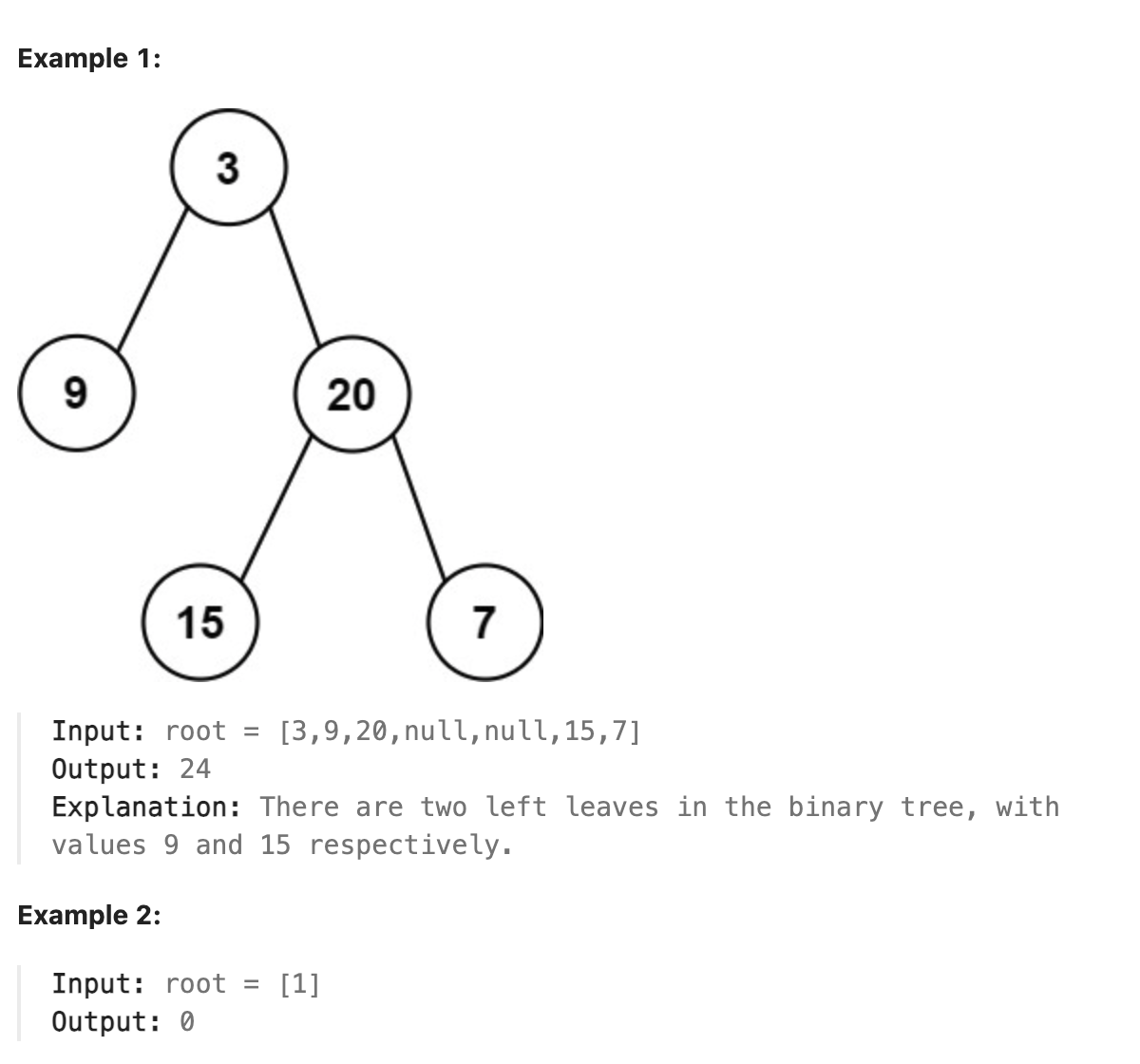
Given the root of a binary tree, return the sum of all left leaves.
|
||||
|
||||
A leaf is a node with no children. A left leaf is a leaf that is the left child of another node.
|
||||
|
||||
|
||||
|
||||
### 题解
|
||||
|
||||
本题是一道简单题, 使用深度优先搜索, 尾序遍历. 遍历的实现可以使用简单的递归函数, 注意对左右两个节点的处理方式不同, 对左节点如果其没有子节点则将值加到结果中, 对右节点则直接继续遍历即可.
|
||||
|
||||
### 代码
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func sumOfLeftLeaves(root *TreeNode) int {
|
||||
result := leftfirst(root)
|
||||
return result
|
||||
}
|
||||
|
||||
func leftfirst(root *TreeNode)int{
|
||||
sum := 0
|
||||
if root.Left != nil && root.Left.Left == nil && root.Left.Right == nil{
|
||||
sum += root.Left.Val
|
||||
}else if root.Left != nil{
|
||||
sum += leftfirst(root.Left)
|
||||
}
|
||||
if root.Right != nil{
|
||||
sum += leftfirst(root.Right)
|
||||
}
|
||||
return sum
|
||||
}
|
||||
```
|
||||
|
||||
Reference in New Issue
Block a user