leetcode update

content/posts/leetcode.md

@@ -16386,3 +16386,183 @@ public:
     }
 };
 ```
+
+## day231 2024-10-25
+
+### 1233. Remove Sub-Folders from the Filesystem
+
+Given a list of folders folder, return the folders after removing all sub-folders in those folders. You may return the answer in any order.
+
+If a folder[i] is located within another folder[j], it is called a sub-folder of it. A sub-folder of folder[j] must start with folder[j], followed by a "/". For example, "/a/b" is a sub-folder of "/a", but "/b" is not a sub-folder of "/a/b/c".
+
+The format of a path is one or more concatenated strings of the form: '/' followed by one or more lowercase English letters.
+
+For example, "/leetcode" and "/leetcode/problems" are valid paths while an empty string and "/" are not.
+
+![1025zSXMNTpsIW7F](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1025zSXMNTpsIW7F.png)
+
+### 题解
+
+本题使用前缀树可解，将文件夹的每一级的路径名视为前缀树中的一个字符串节点，对于遍历到的新的路径，如果路径已经在前缀树中存在，证明其上层文件夹路径已经存在，则该路径可以移除。不存在则在前缀树中创建一个新的路径。
+
+### 代码
+
+```cpp
+class Solution {
+public:
+    vector<string> removeSubfolders(vector<string>& folder) {
+        // 将文件夹路径排序，这样父文件夹会在子文件夹之前处理
+        sort(folder.begin(), folder.end());
+        TrieNode* root = new TrieNode();
+        vector<string> result;
+
+        for (const string& path : folder) {
+            vector<string> components = split(path, '/');
+            if (insert(root, components)) {
+                // 如果插入成功（不是子文件夹），则将路径加入结果中
+                result.push_back(path);
+            }
+        }
+
+
+        return result;
+    }
+
+private:
+    class TrieNode {
+    public:
+        unordered_map<string, TrieNode*> children;
+        bool isEnd;
+        TrieNode() : isEnd(false) {}
+    };
+
+    vector<string> split(const string& s, char delimiter) {
+        vector<string> tokens;
+        int i = 0;
+        while (i < s.size()) {
+            if (s[i] == delimiter) {
+                i++;
+            } else {
+                int j = i;
+                while (j < s.size() && s[j] != delimiter) j++;
+                tokens.push_back(s.substr(i, j - i));
+                i = j;
+            }
+        }
+        return tokens;
+    }
+
+    // 插入路径到前缀树中，返回是否成功插入
+    bool insert(TrieNode* root, const vector<string>& components) {
+        TrieNode* node = root;
+        for (const string& component : components) {
+            if (node->isEnd) {
+                // 当前节点是一个文件夹的结束，后续的是子文件夹，跳过
+                return false;
+            }
+            if (node->children.find(component) == node->children.end()) {
+                node->children[component] = new TrieNode();
+            }
+            node = node->children[component];
+        }
+        node->isEnd = true;
+        return true;
+    }
+
+
+};
+
+```
+
+## day232 2024-10-26
+
+### 2458. Height of Binary Tree After Subtree Removal Queries
+
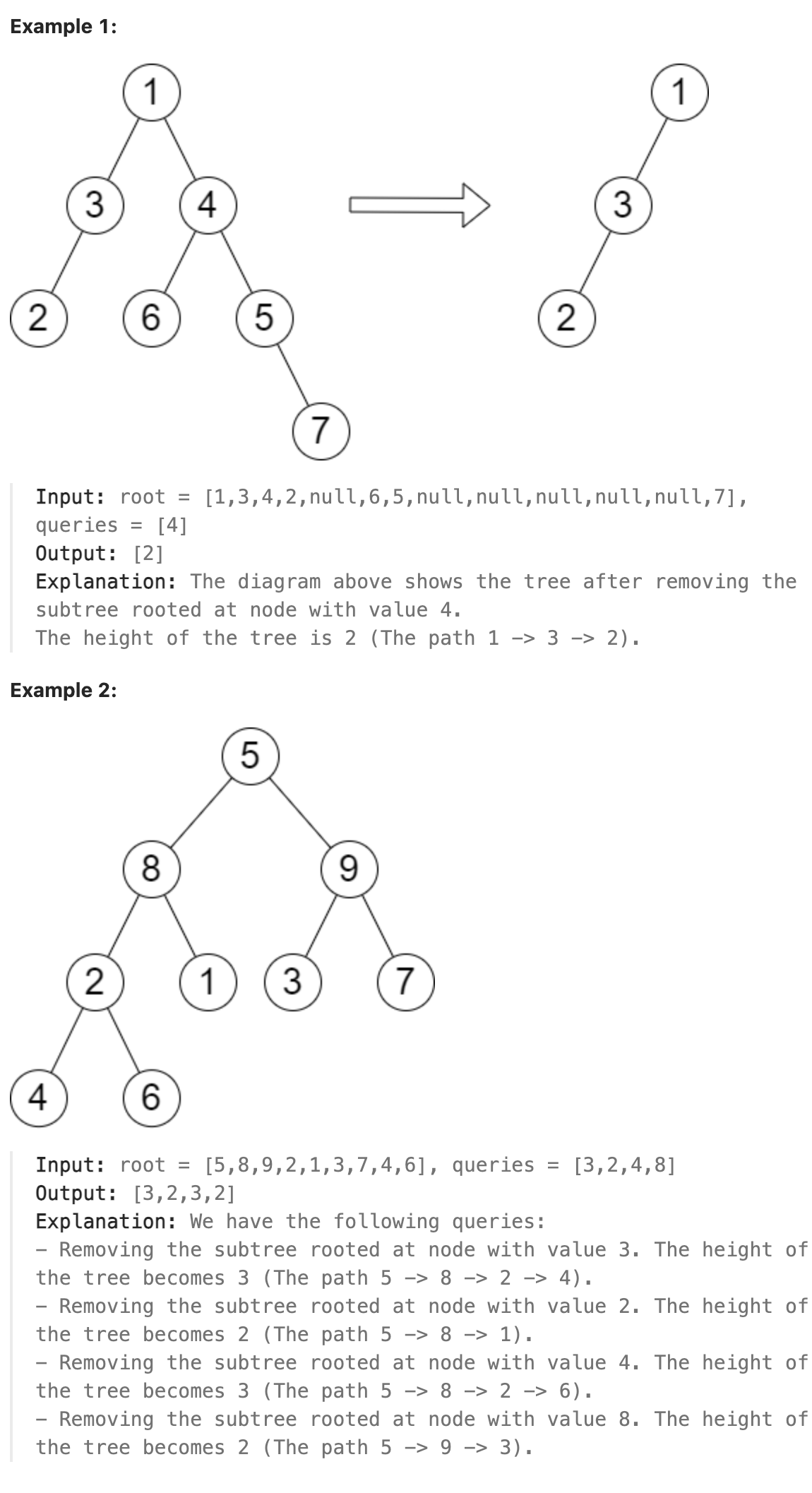
+You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.
+
+You have to perform m independent queries on the tree where in the ith query you do the following:
+
+Remove the subtree rooted at the node with the value queries[i] from the tree. It is guaranteed that queries[i] will not be equal to the value of the root.
+Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.
+
+Note:
+
+The queries are independent, so the tree returns to its initial state after each query.
+The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.
+
+![1026ce2K07Jru8CR](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1026ce2K07Jru8CR.png)
+
+### 题解
+
+本题是一道难题，注意题目中明确说明各个节点的值不同，因此可以考虑通过某种方式将所有节点的一些性质保存下来，避免对树的重复遍历。在遍历过程中可以将到某个节点的高度（相当于从根节点到该节点的高度）保存下来传递给目标节点，同时对该节点极其子树进行遍历可以返回这棵子树的高度（相当于该节点到对应的树的分支的叶子节点即树底的高度），二者之和就是从根节点开始经过该子节点的子树的高度。那么对于树中同一层的所有节点都可以得到这个高度。
+
+考虑树中同一层的节点，我们只需了解该层所有节点中对应的经过节点的所有树高度中的最大树高度和次大树高读（二者可以相同，表示经过两个不同节点均可得到最大树高度）即可确定每一个节点对应的子树如果被删除剩余树的最大高度。如果节点对应的高度为最大树高度，删掉以该节点为根的子树后整棵树的高度即为次大树高度，否则删掉节点为根对应的子树后整棵树的高度为最大树高度。
+
+上述情况适用于同一层有多个节点的情况，同一层有多个节点时因为从根节点当该层所有节点的高度相同，所以删掉该层某个节点后整棵树的最大高度一定从其他节点对应的子树中取得，但当某一层只有一个节点时，删掉该节点及其子树会导致整棵树的高度改变，最大高度为根节点到该节点父节点的高度，即这个唯一节点上面的树的高度。因此要注意处理某一层只有一个节点的情况。
+
+要得到树中经过某个节点的子树的高度，需要dfs，而要对树中每一层的节点进行分析确定删掉某个节点对应的子树后剩余的树高需要bfs，正是题目中明确说明节点值各不相同，因此可以先通过dfs得到各个节点对应的树高并保存，再通过bfs计算删掉某个节点后的剩余树高并保存。最终只需遍历queries数组直接根据被删除的节点值查询答案。
+
+### 代码
+
+```cpp
+class Solution {
+public:
+    vector<int> treeQueries(TreeNode* root, vector<int>& queries) {
+        vector<int> result(100001, 0);
+        height.resize(100001, 0);
+        int maxheight = dfs(root, 0);
+        vector<TreeNode*> layer;
+        vector<TreeNode*> layer2;
+        layer.push_back(root);
+        int currentDepth = 0;
+        while (!layer.empty()) {
+            vector<TreeNode*>().swap(layer2);
+            int max1 = 0;
+            int max2 = 0;
+            for (auto node : layer) {
+                if (height[node->val] > max1) {
+                    max2 = max1;
+                    max1 = height[node->val];
+                } else if (height[node->val] > max2) {
+                    max2 = height[node->val];
+                }
+                if (node->left != nullptr) {
+                    layer2.push_back(node->left);
+                }
+                if (node->right != nullptr) {
+                    layer2.push_back(node->right);
+                }
+            }
+            for (auto node : layer) {
+                if (layer.size() == 1) {
+                    // 如果这一层只有一个节点，结果是上一层的高度
+                    result[node->val] = currentDepth - 1;
+                } else {
+                    result[node->val] = height[node->val] == max1 ? max2 : max1;
+                }
+            }
+            swap(layer, layer2);
+            currentDepth++;
+        }
+        vector<int> returnvector;
+        for (int node : queries) {
+            returnvector.push_back(result[node]);
+        }
+        return returnvector;
+    }
+
+private:
+    vector<int> height;
+
+    int dfs(TreeNode* root, int depth) {
+        if (root == nullptr) {
+            return depth - 1;
+        }
+        int lefth = dfs(root->left, depth + 1);
+        int righth = dfs(root->right, depth + 1);
+        height[root->val] = max({lefth, righth, depth});
+        return height[root->val];
+    }
+};
+
+```