leetcode update

content/posts/leetcode.md

@@ -16610,24 +16610,28 @@ public:
 ```
 
 ## day234 2024-10-28
-### 2501. Longest Square Streak in an Array 
+
+### 2501. Longest Square Streak in an Array
+
 You are given an integer array nums. A subsequence of nums is called a square streak if:
 
 The length of the subsequence is at least 2, and
 after sorting the subsequence, each element (except the first element) is the square of the previous number.
 Return the length of the longest square streak in nums, or return -1 if there is no square streak.
 
-A subsequence is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements. 
+A subsequence is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
 
 ![10283MKmcTHyw2Ig](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/10283MKmcTHyw2Ig.png)
 
 ### 题解
+
 本题先排序，因为我们要找的其实也是一个有序子序列（后一个数均是前一个数的平方，当然比前面的数字更大），在乱序的情况下很难通过一次遍历找到这样的序列，乱序时可能会遇到一个很大的数还需要后面判断是否有它的因子和以它为因子的数，这样我们要处理更多的可能性，而有序我们只需在遍历时判断是否是以前遇到过的数字的平方。
 
 这里可以使用一个队列用于存放遍历过的数字的平方数和该数字对应的子序列当前的长度，遍历有序数组，判断当前数字是否是队列头部的数字，如果是则将头部弹出并将当前序列长度加1，同时向队列末尾插入当前弹出的数字的平方数。如果当前数字比队列头部数字大则同样弹出队列头部，如果比队列头部数字小则向队列末尾插入当前数字的平方数并将子队列长度设置为1。
 
 ### 代码
-```cpp 
+
+```cpp
 class Solution {
 public:
     int longestSquareStreak(vector<int>& nums) {
@@ -16658,26 +16662,31 @@ public:
     }
 };
 ```
+
 ## day235 2024-10-29
-### 2684. Maximum Number of Moves in a Grid 
+
+### 2684. Maximum Number of Moves in a Grid
+
 You are given a 0-indexed m x n matrix grid consisting of positive integers.
 
 You can start at any cell in the first column of the matrix, and traverse the grid in the following way:
 
 From a cell (row, col), you can move to any of the cells: (row - 1, col + 1), (row, col + 1) and (row + 1, col + 1) such that the value of the cell you move to, should be strictly bigger than the value of the current cell.
-Return the maximum number of moves that you can perform. 
+Return the maximum number of moves that you can perform.
 
 ![1029VHe2DV4tTr5N](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1029VHe2DV4tTr5N.png)
 
 ### 题解
+
 本题每次移动时只能移动到自己后面一列的相邻三个方块内，而且必须移动到比当前方格内数字更大的方格中。则假如我们已知到当前方格的最长移动步数，再根据当前方格相邻方格的数字大小判断能否移动，将当前方格最长移动步数+1与相邻方格之前保存的最长步数比较即可知道相邻的几个方格的最长移动步数。在本题中，通过前一个方格的最长移动步数可以更新后面相邻方格的最长移动步数，因此大问题可以转换为从前一个方格移动到后面相邻方格过程中方格最长移动步数变化的小问题，这些小问题结构均相同。这样就可以通过循环，通过递推最终得到大问题的解。
 
 具体而言，构造一个和矩阵大小相同的dp数组保存到某个方格的最长步数，因为题目限制起始方格只能在第一列，则先遍历第一列方格，找到能移动的相邻方格，并将dp数组中相邻方格位置处的步数设置为1。再遍历第二列，按照同样的方式更新dp数组中第三列的步数值，以此类推，在更新过程中将更新的步数与最大步数比较，不断更新最大步数，最终返回最大步数。
 
-实现过程中要注意一个问题，即在遍历每一列时只有当前那些可以从前一列访问到的格子需要继续向后移动，而那些从前一列中无法访问到的格子是直接忽略的，因为题目要求起点必须从第一列开始，因此从第一列开始移动过程中所有不可达的格子都无需再访问，再访问就会导致从中间某一列的格子开始。同样基于这个原因，遍历过程中可以实现早停，如果某一列中所有格子在从第一列移动到该列时均已经无法访问，则可以结束遍历直接返回结果，因为不会再有**从第一列起始**的更长的路径了。 
+实现过程中要注意一个问题，即在遍历每一列时只有当前那些可以从前一列访问到的格子需要继续向后移动，而那些从前一列中无法访问到的格子是直接忽略的，因为题目要求起点必须从第一列开始，因此从第一列开始移动过程中所有不可达的格子都无需再访问，再访问就会导致从中间某一列的格子开始。同样基于这个原因，遍历过程中可以实现早停，如果某一列中所有格子在从第一列移动到该列时均已经无法访问，则可以结束遍历直接返回结果，因为不会再有**从第一列起始**的更长的路径了。
 
 ### 代码
-```cpp 
+
+```cpp
 class Solution {
 public:
     int maxMoves(vector<vector<int>>& grid) {
@@ -16695,7 +16704,7 @@ public:
                         maxmove = max(dp[j+row][i+1], maxmove);
                         successmove = true;
                     }
-                } 
+                }
             }
             if (!successmove){
                 break;
@@ -16705,3 +16714,197 @@ public:
     }
 };
 ```
+
+## day236 2024-10-30
+
+### 1671. Minimum Number of Removals to Make Mountain Array
+
+You may recall that an array arr is a mountain array if and only if:
+
+arr.length >= 3
+There exists some index i (0-indexed) with 0 < i < arr.length - 1 such that:
+arr[0] < arr[1] < ... < arr[i - 1] < arr[i]
+arr[i] > arr[i + 1] > ... > arr[arr.length - 1]
+Given an integer array nums, return the minimum number of elements to remove to make nums a mountain array.
+
+![1030CgyOV9qqLX1e](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1030CgyOV9qqLX1e.png)
+
+### 题解
+
+如果做过接雨水这个经典题目，做这道题时可能会有一个相似的初始思路，即通过正向遍历将以下标i为结尾的递增最长递增子序列长度求出并保存，再反向遍历将以下标i起始的递减最长子序列长度求出并保存（相当于反向求递增最长子序列长度）。随后再遍历一次数组，将下标i对应的之前求出的两个长度加和再减一（i被重复计算）即得经过下标i的最长的“山峰”数组的长度，遍历一遍即得数组中最长的“山峰”长度，用总长度与该长度做差即得最终结果。
+
+如何求出递增最长子序列，假如已知i之前的小于arr\[i\]的数字对应下标的递增最长子序列为下标j对应的子序列，则i对应的最长递增子序列等于j对应的子序列长度+1。但考虑i之前比arr\[i\]小的最靠近i的数字对应的子序列未必最长，而我们也无法确定哪个数字对应的子序列最长（考虑如下情况，如序列3,1,2,3,2,5。则在5之前对应的序列最长的应该为1，2，3长度为3。）因此需要遍历i之前所有小于arr\[i\]的数字和其对应的子序列长度，取其中最长的长度，将其+1作为i对应的最长子序列长度。
+
+注意本题删除后得到的数组必须是“山峰”，因此对于到i仅单调增或者从i开始单调减的情况均不考虑。最终计算结果时要注意处理这种情况。
+
+### 代码
+
+```cpp
+class Solution {
+public:
+    int minimumMountainRemovals(vector<int>& nums) {
+        vector<int> normal(nums.size(),0);
+        vector<int> reverse(nums.size(),0);
+        for (int i=0;i<nums.size();i++){
+            int maxl = 0;
+            for(int j=0;j<i;j++){
+                if (nums[j] < nums[i]){
+                    maxl = max(maxl, normal[j]);
+                }
+            }
+            normal[i] = maxl+1;
+        }
+        for (int i=nums.size()-1;i>=0;i--){
+            int maxl = 0;
+            for(int j=nums.size()-1;j>i;j--){
+                if (nums[j]<nums[i]){
+                    maxl = max(maxl, reverse[j]);
+                }
+            }
+            reverse[i] = maxl+1;
+        }
+        int maxlen = 0;
+        for (int i=0;i<nums.size();i++){
+            // make i a mountain
+            if (normal[i] > 1 && reverse[i] > 1 && normal[i]+reverse[i] > maxlen){
+                maxlen = normal[i]+reverse[i];
+            }
+        }
+        return nums.size()-maxlen+1;
+    }
+};
+```
+
+## day237 2024-10-31
+
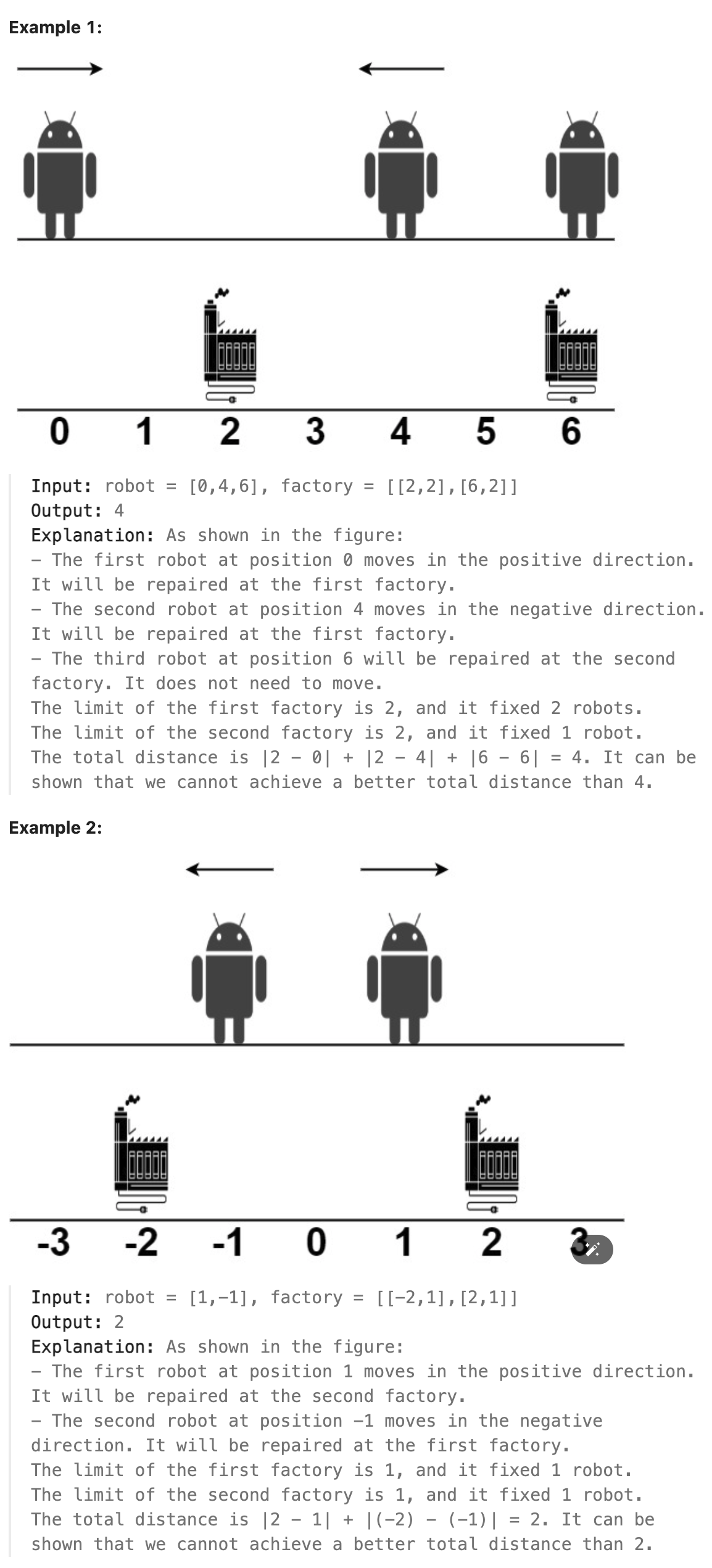
+### 2463. Minimum Total Distance Traveled
+
+There are some robots and factories on the X-axis. You are given an integer array robot where robot[i] is the position of the ith robot. You are also given a 2D integer array factory where factory[j] = [positionj, limitj] indicates that positionj is the position of the jth factory and that the jth factory can repair at most limitj robots.
+
+The positions of each robot are unique. The positions of each factory are also unique. Note that a robot can be in the same position as a factory initially.
+
+All the robots are initially broken; they keep moving in one direction. The direction could be the negative or the positive direction of the X-axis. When a robot reaches a factory that did not reach its limit, the factory repairs the robot, and it stops moving.
+
+At any moment, you can set the initial direction of moving for some robot. Your target is to minimize the total distance traveled by all the robots.
+
+Return the minimum total distance traveled by all the robots. The test cases are generated such that all the robots can be repaired.
+
+Note that
+
+All robots move at the same speed.
+If two robots move in the same direction, they will never collide.
+If two robots move in opposite directions and they meet at some point, they do not collide. They cross each other.
+If a robot passes by a factory that reached its limits, it crosses it as if it does not exist.
+If the robot moved from a position x to a position y, the distance it moved is |y - x|.
+
+![1031hTVL7LwAFYOv](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1031hTVL7LwAFYOv.png)
+
+### 题解
+
+本题是一道难题，假如每个工厂能够维修的机器人个数是无限的，则本题可以直接通过贪心来解决，但本题中每个工厂能够维修的机器人个数是有限的，则此时的局部最优未必可以最终做到全局最优，因为要考虑工厂维修个数的限制，如一个机器人位于两个工厂1，2之间，尽管可能其离2更近，但若后面还有一个机器人离2同样近且2只能维修一个，那么可能将这个机器人派往1维修最终得到的全局结果是最佳的。
+
+既然不知道对于每个工厂来说，维修几个机器人最终能够得到一个全局最优解，那就将所有的情况都保存下来，下一个工厂再根据上一个工厂的情况得到基于上一个工厂的最优情况。这样若知道了第n-1个工厂的全部情况，则相当于已经处理了全部n-1个工厂，就可以得到n个工厂的全部情况。
+
+这里我们要考虑一个问题，以三个工厂为例，为什么处理了两个工厂的情况后，第三个工厂仅根据第二个工厂的情况就能得到全局的最优情况。假如每个工厂都只能维修两个机器人，三个工厂从左到右分别为1，2，3。机器人从左到右依次为a,b,c,d,e。则若工厂1维修了机器人a，此时工厂2要考虑的情况就是可以选择维修0个，1个，2个机器人，其选择维修的机器人必定从最左侧没有被维修的机器人（此时是b）开始。这里包含的隐藏信息就是，在将有限的机器人分配给左右两个工厂时，若分配的个数是固定的，则左侧的机器人选择左侧的工厂，右侧的机器人选择右侧的工厂得到的路径和一定比右侧的机器人选择左侧的工厂，左侧的机器人选择右侧的工厂近。这个性质和单调性有关，在两个序列保持单调的情况下，相同方向的匹配会得到更优的结果，这种性质也与重排不等式有几分相似。
+
+基于此，将机器人和工厂排序，遍历工厂，根据前一个工厂的最优情况计算当前工厂在维修不同个数机器人情况下的最优情况，若工厂n维修不同个数机器人得到的最小总距离为数组dp，则工厂n+1维修机器人的情况为
+
+$$
+
+dp[n+1][j] = \min_{k=0}^j \{dp[n][k] + \sum_{i=k+1}^j |location\_robot[i] - location\_fac[n+1]|\}
+
+
+$$
+
+其中：
+
+- n+1 表示当前处理的工厂编号
+- j 表示需要修理的机器人总数
+- k 表示前n个工厂修理的机器人数量
+- \sum\_{i=k+1}^j |location_robot[i] - location_fac[n+1]| 表示第n+1个工厂修理从第k+1到第j个机器人的总距离
+
+但此时会发现，按照这样的思路，在计算的时候其实并不知道哪里是该工厂应该遍历的机器人的最左侧，因为只知道前一个工厂对维修不同个数机器人的最优情况，那么可以将第n个工厂维修前j个机器人的最小距离保存起来，每次都从第一个机器人开始遍历维修前n个工厂能维修的机器人总数的所有情况，得到该工厂能维修的前j+limit个机器人的所有情况并更新前j+limit个机器人被维修需要的最短距离。
+
+最终取最后一个机器人被修好的最短总距离。
+
+### 代码
+
+```cpp
+class Solution {
+public:
+    long long minimumTotalDistance(vector<int>& robot, vector<vector<int>>& factory) {
+        int M = robot.size();
+        int N = factory.size();
+        sort(robot.begin(), robot.end());
+        sort(factory.begin(), factory.end());
+        int cum_limit = 0;
+
+        // dp[j]: minimum total distance to repair first j robots
+        vector<long long> dp(M+1, LLONG_MAX);
+        dp[0] = 0;
+
+        for(int n = 0; n < N; ++n) {
+            int limit = factory[n][1];
+            int pos = factory[n][0];
+            int max_j = min(cum_limit, M);
+            // We only need to consider up to all factory limits' sum or robots num
+            vector<long long> new_dp(dp);
+            for(int j = 0; j <= max_j; ++j) {
+                if(dp[j] == LLONG_MAX) continue;
+                long long cost = 0;
+                // Try to assign up to 'limit' robots to current factory
+                for(int k = 1; k <= limit && j + k <= M; ++k) {
+                    cost += abs(robot[j + k - 1] - pos);
+                    if(new_dp[j + k] > dp[j] + cost) {
+                        new_dp[j + k] = dp[j] + cost;
+                    }
+                }
+            }
+            cum_limit += limit;
+            dp = move(new_dp);
+        }
+        return dp[M];
+    }
+};
+```
+
+## day238 2024-11-01
+
+### 1957. Delete Characters to Make Fancy String
+
+A fancy string is a string where no three consecutive characters are equal.
+
+Given a string s, delete the minimum possible number of characters from s to make it fancy.
+
+Return the final string after the deletion. It can be shown that the answer will always be unique.
+
+![1101eF6yDjgCcy2A](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1101eF6yDjgCcy2A.png)
+
+### 题解
+
+本题是一道简单题只需每次遇到超过两个连续的相同字符时将该字符忽略。用一个变量记录当前字符，另一个变量记录字符重复的次数。若次数为2且新字符等于当前字符则忽略新字符，如此直到字符串末尾即构造得到新字符串。
+
+### 代码
+
+```cpp
+class Solution {
+public:
+    string makeFancyString(string s) {
+        string result;
+        char current = s[0];
+        int count = 0;
+        for (auto ch : s){
+            if (count == 2 && current == ch){
+                continue;
+            }else if(current == ch){
+                count++;
+            }else{
+                current = ch;
+                count = 1;
+            }
+            result.push_back(ch);
+        }
+        return result;
+    }
+};
+```