mirror of
https://gitlab.com/game-loader/hugo.git
synced 2025-12-30 12:32:03 +08:00
leetcode update
This commit is contained in:
@ -15926,3 +15926,417 @@ private:
|
|||||||
而且在本题长度最多16的情况下,对可能存在多个重复数字情况的优化并没有效率上的提升,反而因为增加了更多的预处理和递归过程中的判断不如这个简单的方式来的快。因此任何优化都要结合具体场景,如果现在题目输入变为数组长度长得多但存在很多重复数字的情况,那么对重复数字的情况进行优化可能就会比单纯的直接枚举要快。
|
而且在本题长度最多16的情况下,对可能存在多个重复数字情况的优化并没有效率上的提升,反而因为增加了更多的预处理和递归过程中的判断不如这个简单的方式来的快。因此任何优化都要结合具体场景,如果现在题目输入变为数组长度长得多但存在很多重复数字的情况,那么对重复数字的情况进行优化可能就会比单纯的直接枚举要快。
|
||||||
|
|
||||||
另外则是,尽管有时候我们思考过程中可能会出现一些错误的或不那么好的思路,但这些过程并非没有意义,只有经过了这样的思考,才能更加深入的理解问题出在哪里,明白什么样的问题用什么样的思想。
|
另外则是,尽管有时候我们思考过程中可能会出现一些错误的或不那么好的思路,但这些过程并非没有意义,只有经过了这样的思考,才能更加深入的理解问题出在哪里,明白什么样的问题用什么样的思想。
|
||||||
|
|
||||||
|
## day225 2024-10-19
|
||||||
|
|
||||||
|
### 1545. Find Kth Bit in Nth Binary String
|
||||||
|
|
||||||
|
Given two positive integers n and k, the binary string Sn is formed as follows:
|
||||||
|
|
||||||
|
S1 = "0"
|
||||||
|
Si = Si - 1 + "1" + reverse(invert(Si - 1)) for i > 1
|
||||||
|
Where + denotes the concatenation operation, reverse(x) returns the reversed string x, and invert(x) inverts all the bits in x (0 changes to 1 and 1 changes to 0).
|
||||||
|
|
||||||
|
For example, the first four strings in the above sequence are:
|
||||||
|
|
||||||
|
S1 = "0"
|
||||||
|
S2 = "011"
|
||||||
|
S3 = "0111001"
|
||||||
|
S4 = "011100110110001"
|
||||||
|
Return the kth bit in Sn. It is guaranteed that k is valid for the given n.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
### 题解
|
||||||
|
|
||||||
|
本题因为n最多只到20,所以理论上可以直接将S20的字符串是什么算出来,然后直接“查表”。对于k直接返回字符串的第k位的字符即可。
|
||||||
|
|
||||||
|
因为题目代码有提交长度限制,S20过长所以上面的方式不可行。故可以直接模拟构造过程构造出需要的字符串并取k位,但对于一个很小的k可能并不需要给定的n,故可以在构造过程中记录当前构造的字符串长度,当长度大于等于k时即停止构造并返回k位字符。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
char findKthBit(int n, int k) {
|
||||||
|
int len = 1;
|
||||||
|
string sn = "0";
|
||||||
|
while (len < k){
|
||||||
|
string rev;
|
||||||
|
for (int i=len-1;i>=0;i--){
|
||||||
|
rev.push_back(sn[i] ^ 1);
|
||||||
|
}
|
||||||
|
sn += "1"+rev;
|
||||||
|
len = len*2 + 1;
|
||||||
|
}
|
||||||
|
return sn[k-1];
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
### 总结
|
||||||
|
|
||||||
|
这时可以想到,构造字符串本身是一件非常耗时的任务,而我们其实只需要找到某一位字符是什么,其他字符都没用。那是否可以直接通过计算推断出某一位字符是什么呢?当然是可以的。我们思考构造字符串的过程,就是以1作为中间分割左右字符串互成与1异或后的镜像字符串。分割的1右侧的字符串是由左侧的字符串通过构造得来的,那么我们就可以直接将原本的落在右侧字符串某一位的k转换成左侧字符串的某一位(如001 和 011。则右侧的0对应左侧最后的1,右侧的两个1分别对应左侧的两个0。)则我们只需要知道到k的时候一共发生了几次转换即可得出最终k是什么。
|
||||||
|
给定n最终得到的字符串长度为2^n-1(找规律,sn = 2\*s(n-1)+1)。则可以将字符串sn分为左右两部分,如果k的位置在sn的左半部分,则可退化到解决n-1,k的问题。如果在右半部分,则可以根据位置转换到左半部分并退化到解决n-1,new"k"的问题(新的k的位置根据字符串长度和原来的k计算出来),只是结果需要翻转一次。如果在正中间,那就是中间添加的字符"1"。如此将问题不断分解直到退化到n=1或者正巧遇到字符在中间即可得到解决。
|
||||||
|
解法为按照上面的思路不断将k和n减小,记录过程中k被翻转的次数。最终停止问题分解时将得到的原始字符翻转对应的次数(偶数不翻转,奇数翻转)即得最终结果。
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
char findKthBit(int n, int k) {
|
||||||
|
int len = (1 << n) - 1;
|
||||||
|
int count = 0;
|
||||||
|
char bit = '0';
|
||||||
|
|
||||||
|
while (n > 1) {
|
||||||
|
int mid = (len + 1) / 2;
|
||||||
|
|
||||||
|
if (k == mid) {
|
||||||
|
bit = '1';
|
||||||
|
break;
|
||||||
|
}
|
||||||
|
|
||||||
|
if (k > mid) {
|
||||||
|
k = len - k + 1; // 映射到左半部分
|
||||||
|
count++; // 需要翻转
|
||||||
|
}
|
||||||
|
|
||||||
|
n--;
|
||||||
|
len = (1 << n) - 1;
|
||||||
|
}
|
||||||
|
|
||||||
|
// 根据翻转次数决定是否需要翻转最终结果
|
||||||
|
return (count % 2 == 0) ? bit : (bit == '0' ? '1' : '0');
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
## day226 2024-10-20
|
||||||
|
|
||||||
|
### 1106. Parsing A Boolean Expression
|
||||||
|
|
||||||
|
A boolean expression is an expression that evaluates to either true or false. It can be in one of the following shapes:
|
||||||
|
|
||||||
|
't' that evaluates to true.
|
||||||
|
'f' that evaluates to false.
|
||||||
|
'!(subExpr)' that evaluates to the logical NOT of the inner expression subExpr.
|
||||||
|
'&(subExpr1, subExpr2, ..., subExprn)' that evaluates to the logical AND of the inner expressions subExpr1, subExpr2, ..., subExprn where n >= 1.
|
||||||
|
'|(subExpr1, subExpr2, ..., subExprn)' that evaluates to the logical OR of the inner expressions subExpr1, subExpr2, ..., subExprn where n >= 1.
|
||||||
|
Given a string expression that represents a boolean expression, return the evaluation of that expression.
|
||||||
|
|
||||||
|
It is guaranteed that the given expression is valid and follows the given rules.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
### 题解
|
||||||
|
|
||||||
|
本题是一道难题,其实就是一道编译原理中的简单语义分析的题目。解题结构就是将各种不同的表达式分别设计处理函数,并返回该表达式表示的布尔值。在读取字符串的过程中,根据当前读到的字符转入不同的表达式处理函数。
|
||||||
|
具体的表达式处理,以&表达式为例,当读取到的符号为&时,先读入一个左括号并丢掉,随后进入循环,只要没有读取到右括号就不断循环。循环时仍然根据读取的符号进入不同的表达式处理函数,如再次读到一个&则再次进入&表达式处理函数。处理完成得到该子表达式返回的布尔值,如果下一个字符是一个逗号,则移动指针指向逗号后面的字符,并进入下一次循环。
|
||||||
|
用指针可以避免字符串的复制,因为本题只需要解析表达式最终的表达值,所以任何复制都是多余的。
|
||||||
|
这里其实将词法分析的部分也嵌入到了分析当中,因为并没有什么变量之类的多字符,仅有限的几个字符,直接读取并处理。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int index = 0; // 用于跟踪当前处理的字符位置
|
||||||
|
|
||||||
|
bool parseBoolExpr(string expression) {
|
||||||
|
return parseExpr(expression);
|
||||||
|
}
|
||||||
|
|
||||||
|
private:
|
||||||
|
bool parseExpr(const string& expr) {
|
||||||
|
char c = expr[index];
|
||||||
|
if (c == 't') {
|
||||||
|
index++;
|
||||||
|
return true;
|
||||||
|
} else if (c == 'f') {
|
||||||
|
index++;
|
||||||
|
return false;
|
||||||
|
} else if (c == '!') {
|
||||||
|
return parseNot(expr);
|
||||||
|
} else if (c == '&') {
|
||||||
|
return parseAnd(expr);
|
||||||
|
} else if (c == '|') {
|
||||||
|
return parseOr(expr);
|
||||||
|
}
|
||||||
|
return false;
|
||||||
|
}
|
||||||
|
|
||||||
|
bool parseNot(const string& expr) {
|
||||||
|
index += 2; // 跳过 '!('
|
||||||
|
bool result = !parseExpr(expr);
|
||||||
|
index++; // 跳过 ')'
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
|
||||||
|
bool parseAnd(const string& expr) {
|
||||||
|
index += 2; // 跳过 '&('
|
||||||
|
bool result = true;
|
||||||
|
while (expr[index] != ')') {
|
||||||
|
result &= parseExpr(expr);
|
||||||
|
if (expr[index] == ',') index++;
|
||||||
|
}
|
||||||
|
index++; // 跳过 ')'
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
|
||||||
|
bool parseOr(const string& expr) {
|
||||||
|
index += 2; // 跳过 '|('
|
||||||
|
bool result = false;
|
||||||
|
while (expr[index] != ')') {
|
||||||
|
result |= parseExpr(expr);
|
||||||
|
if (expr[index] == ',') index++;
|
||||||
|
}
|
||||||
|
index++; // 跳过 ')'
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
### 总结
|
||||||
|
|
||||||
|
本题如果熟悉编译原理相关的知识并做过一些简单的词法分析,语法分析和语义分析的手动实现,那么本题就不算一道难题了。
|
||||||
|
|
||||||
|
## day227 2024-10-21
|
||||||
|
|
||||||
|
### 1593. Split a String Into the Max Number of Unique Substrings
|
||||||
|
|
||||||
|
Given a string s, return the maximum number of unique substrings that the given string can be split into.
|
||||||
|
|
||||||
|
You can split string s into any list of non-empty substrings, where the concatenation of the substrings forms the original string. However, you must split the substrings such that all of them are unique.
|
||||||
|
|
||||||
|
A substring is a contiguous sequence of characters within a string.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
### 题解
|
||||||
|
|
||||||
|
本题最初会想到可以使用贪心+哈希表的方式解题。考虑题目要求最多能分割成多少个不一样的子字符串,则每次分割分割出一个尽可能短的字符串,在总长固定的情况下,就能得到尽可能多的字符串。但本题中局部最优并不一定是全局最优,这是因为我们分割时的遍历是从前向后遍历的,而能分割出数量最多的字符串可能将比较短的字符串放在中间位置才能得到。即分割出的比较短的字符串不一定总在整个字符串的前面。因此贪心不是总能得到最优解。
|
||||||
|
|
||||||
|
则可以考虑遍历所有的分割组合找到分割个数最多的组合。可以使用递归结合回溯的方式遍历所有的分割组合。递归函数中分割时从当前的起始位置开始,依次分割长度为1,2...的字符串,判断当前分割出来的字符串是否与之前分割的字符串有重复,没有则将分割出来的字符串放入set,同时从新的起始位置开始调用递归函数进行后面的分割,得到后面分割的字符串个数+1与当前的分割最大值比较并更新最大值。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int maxUniqueSplit(string s) {
|
||||||
|
unordered_set<string> exist;
|
||||||
|
return backtrack(s, 0, exist);
|
||||||
|
}
|
||||||
|
|
||||||
|
private:
|
||||||
|
int backtrack(const string& s, int start, unordered_set<string>& exist) {
|
||||||
|
if (start == s.length()) {
|
||||||
|
return 0;
|
||||||
|
}
|
||||||
|
|
||||||
|
int maxSplits = 0;
|
||||||
|
for (int i = start; i < s.length(); i++) {
|
||||||
|
string current = s.substr(start, i - start + 1);
|
||||||
|
if (exist.find(current) == exist.end()) {
|
||||||
|
exist.insert(current);
|
||||||
|
int splits = 1 + backtrack(s, i + 1, exist);
|
||||||
|
maxSplits = max(maxSplits, splits);
|
||||||
|
exist.erase(current);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
return maxSplits;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
### 总结
|
||||||
|
|
||||||
|
从上面的过程也可以看出,有些分割是没必要继续进行的,如从头开始分割时分割的第一个字符串的长度即为整个字符串长度减一,这种情况必然只能得到两个字符串,同理分割长度为整个字符串长度减二时,整体分割完最多也只能得到三个字符串。那么什么时候可以剪枝呢,即当当前分割的字符串个数加上剩余的字符串长度小于等于当前分割个数的最大值时可以提前结束本次分割(剩余字符串长度表示将剩余字符串按每个单独字符进行分割得到的字符串个数,即剩余字符串能分割得到的最多个数)
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int maxUniqueSplit(string s) {
|
||||||
|
unordered_set<string> seen;
|
||||||
|
int maxCount = 0;
|
||||||
|
backtrack(s, 0, seen, 0, maxCount);
|
||||||
|
return maxCount;
|
||||||
|
}
|
||||||
|
|
||||||
|
private:
|
||||||
|
void backtrack(const string& s, int start, unordered_set<string>& seen,
|
||||||
|
int count, int& maxCount) {
|
||||||
|
if (count + (s.size() - start) <= maxCount) return;
|
||||||
|
|
||||||
|
if (start == s.size()) {
|
||||||
|
maxCount = max(maxCount, count);
|
||||||
|
return;
|
||||||
|
}
|
||||||
|
|
||||||
|
for (int end = start + 1; end <= s.size(); ++end) {
|
||||||
|
string substring = s.substr(start, end - start);
|
||||||
|
if (seen.find(substring) == seen.end()) {
|
||||||
|
seen.insert(substring);
|
||||||
|
backtrack(s, end, seen, count + 1, maxCount);
|
||||||
|
seen.erase(substring);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
## day228 2024-10-22
|
||||||
|
|
||||||
|
### 2583. Kth Largest Sum in a Binary Tree
|
||||||
|
|
||||||
|
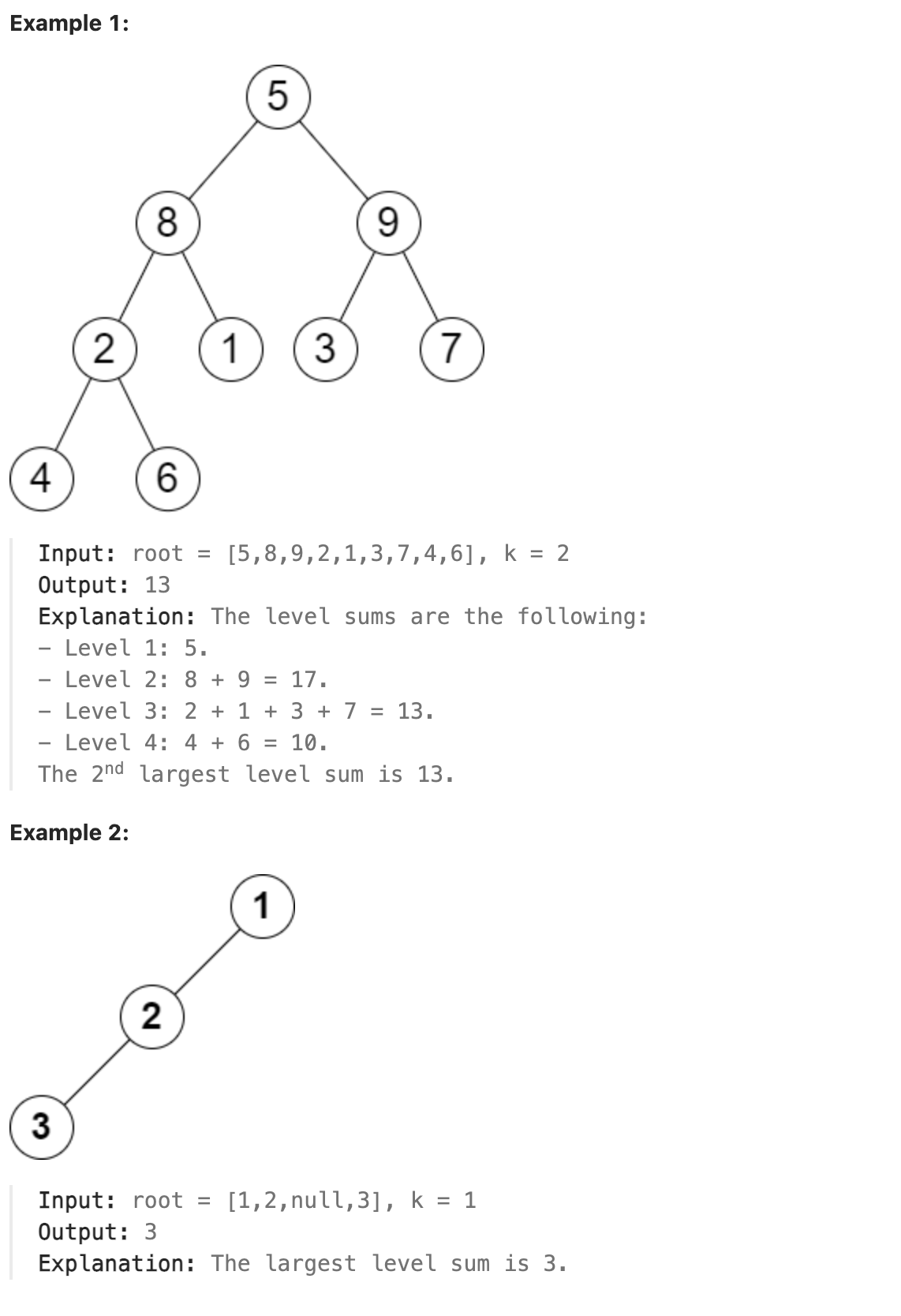
You are given the root of a binary tree and a positive integer k.
|
||||||
|
|
||||||
|
The level sum in the tree is the sum of the values of the nodes that are on the same level.
|
||||||
|
|
||||||
|
Return the kth largest level sum in the tree (not necessarily distinct). If there are fewer than k levels in the tree, return -1.
|
||||||
|
|
||||||
|
Note that two nodes are on the same level if they have the same distance from the root.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 题解
|
||||||
|
|
||||||
|
本题进行二叉树的层序遍历(BFS)对每一层求和并将其全部放入最大堆中,最终根据k将堆顶从堆中弹出k次即得第k大的和。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
/**
|
||||||
|
* Definition for a binary tree node.
|
||||||
|
* struct TreeNode {
|
||||||
|
* int val;
|
||||||
|
* TreeNode *left;
|
||||||
|
* TreeNode *right;
|
||||||
|
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
|
||||||
|
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
|
||||||
|
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
|
||||||
|
* };
|
||||||
|
*/
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
long long kthLargestLevelSum(TreeNode* root, int k) {
|
||||||
|
priority_queue<long long int> heap;
|
||||||
|
queue<TreeNode*> bfs;
|
||||||
|
queue<TreeNode*> bfs2;
|
||||||
|
bfs.push(root);
|
||||||
|
TreeNode* front;
|
||||||
|
while(!bfs.empty()){
|
||||||
|
long long int layer = 0;
|
||||||
|
while(!bfs.empty()){
|
||||||
|
front = bfs.front();
|
||||||
|
layer += front->val;
|
||||||
|
if(front->left != nullptr){
|
||||||
|
bfs2.push(front->left);
|
||||||
|
}
|
||||||
|
if(front->right != nullptr){
|
||||||
|
bfs2.push(front->right);
|
||||||
|
}
|
||||||
|
bfs.pop();
|
||||||
|
}
|
||||||
|
heap.push(layer);
|
||||||
|
swap(bfs,bfs2);
|
||||||
|
}
|
||||||
|
for(;k>1;k--){
|
||||||
|
if(heap.empty()){
|
||||||
|
return -1;
|
||||||
|
}
|
||||||
|
heap.pop();
|
||||||
|
}
|
||||||
|
if(!heap.empty()){
|
||||||
|
return heap.top();
|
||||||
|
}
|
||||||
|
return -1;
|
||||||
|
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
## day229 2024-10-23
|
||||||
|
|
||||||
|
### 2641. Cousins in Binary Tree II
|
||||||
|
|
||||||
|
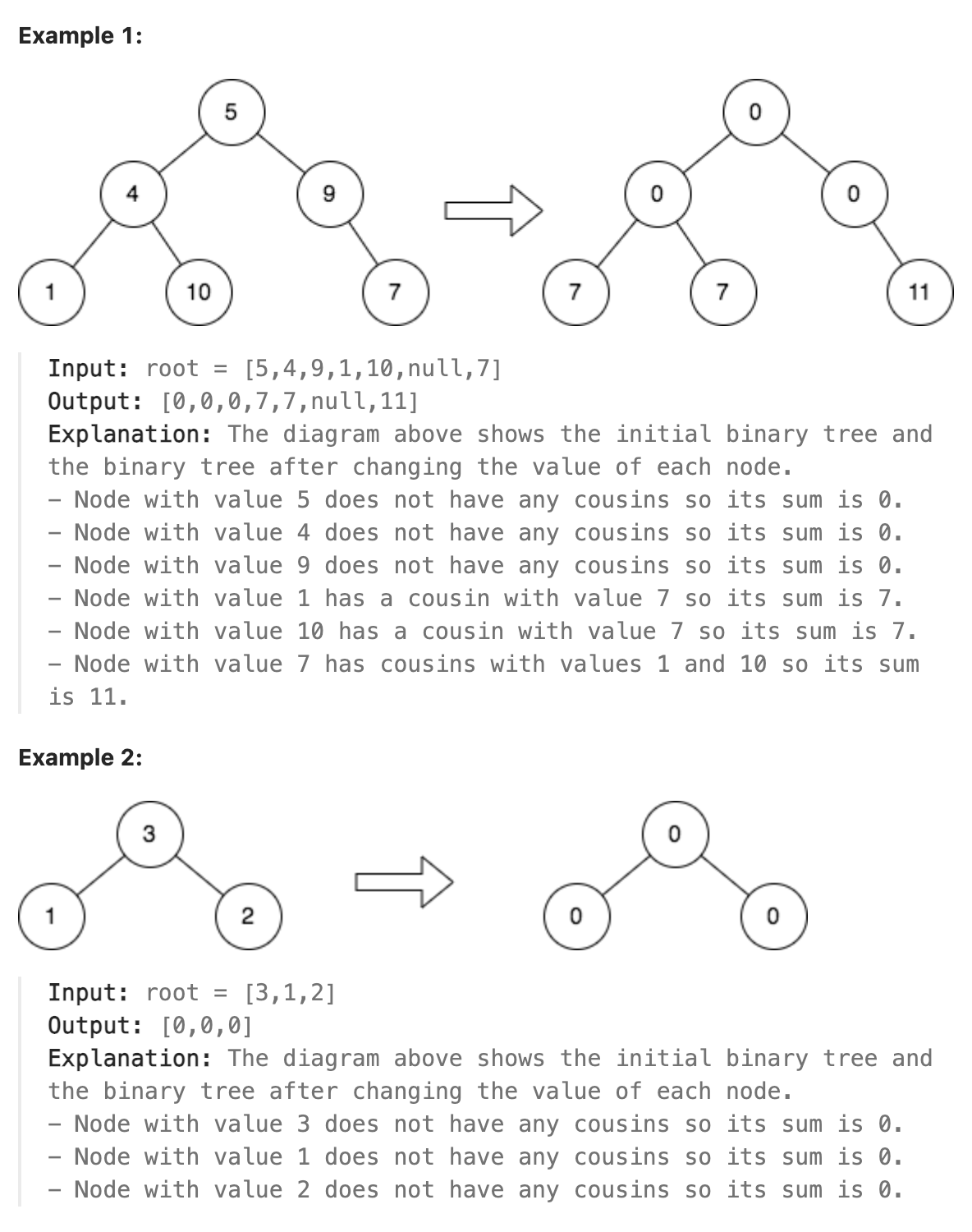
Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins' values.
|
||||||
|
|
||||||
|
Two nodes of a binary tree are cousins if they have the same depth with different parents.
|
||||||
|
|
||||||
|
Return the root of the modified tree.
|
||||||
|
|
||||||
|
Note that the depth of a node is the number of edges in the path from the root node to it.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 题解
|
||||||
|
|
||||||
|
本题不可能在一次遍历的时候就将节点的cousins的值计算出来并赋给节点。因为在遍历某一层的前面的节点时后面的节点还没有遍历到,不可能预知后面节点的值。因此可以遍历两次,第一次先将每一层的总和计算出来并保存(bfs,参考昨天题目的题解),后续遍历时只需用总和减去同一个父节点下的节点的和即得需要赋给节点的值。这里可以使用dfs,在父节点计算出子节点需要被赋的值并递归遍历子节点。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
/**
|
||||||
|
* Definition for a binary tree node.
|
||||||
|
* struct TreeNode {
|
||||||
|
* int val;
|
||||||
|
* TreeNode *left;
|
||||||
|
* TreeNode *right;
|
||||||
|
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
|
||||||
|
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
|
||||||
|
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
|
||||||
|
* };
|
||||||
|
*/
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
vector<long long int> sum;
|
||||||
|
void dfs(TreeNode* root, int targetvalue, int depth){
|
||||||
|
root->val = targetvalue;
|
||||||
|
if(depth == sum.size()){
|
||||||
|
return;
|
||||||
|
}
|
||||||
|
int newtarget = sum[depth];
|
||||||
|
if (root->left != nullptr){
|
||||||
|
newtarget -= root->left->val;
|
||||||
|
}
|
||||||
|
if (root->right != nullptr){
|
||||||
|
newtarget -= root->right->val;
|
||||||
|
}
|
||||||
|
if (root->left != nullptr){
|
||||||
|
dfs(root->left, newtarget, depth+1);
|
||||||
|
}
|
||||||
|
if (root->right != nullptr){
|
||||||
|
dfs(root->right, newtarget, depth+1);
|
||||||
|
}
|
||||||
|
return;
|
||||||
|
}
|
||||||
|
TreeNode* replaceValueInTree(TreeNode* root) {
|
||||||
|
queue<TreeNode*> bfs;
|
||||||
|
queue<TreeNode*> bfs2;
|
||||||
|
bfs.push(root);
|
||||||
|
TreeNode* front;
|
||||||
|
while(!bfs.empty()){
|
||||||
|
long long int layer = 0;
|
||||||
|
while(!bfs.empty()){
|
||||||
|
front = bfs.front();
|
||||||
|
layer += front->val;
|
||||||
|
if(front->left != nullptr){
|
||||||
|
bfs2.push(front->left);
|
||||||
|
}
|
||||||
|
if(front->right != nullptr){
|
||||||
|
bfs2.push(front->right);
|
||||||
|
}
|
||||||
|
bfs.pop();
|
||||||
|
}
|
||||||
|
sum.push_back(layer);
|
||||||
|
swap(bfs,bfs2);
|
||||||
|
}
|
||||||
|
dfs(root,0,1);
|
||||||
|
return root;
|
||||||
|
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|||||||
Reference in New Issue
Block a user