leetcode update

content/posts/leetcode.md

@@ -19768,3 +19768,614 @@ public:
     }
 };
 ```
+## day285 2024-12-18
+### 1475. Final Prices With a Special Discount in a Shop 
+You are given an integer array prices where prices[i] is the price of the ith item in a shop.
+
+There is a special discount for items in the shop. If you buy the ith item, then you will receive a discount equivalent to prices[j] where j is the minimum index such that j > i and prices[j] <= prices[i]. Otherwise, you will not receive any discount at all.
+
+Return an integer array answer where answer[i] is the final price you will pay for the ith item of the shop, considering the special discount.
+
+![1218vjGm9A6dZR7z](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1218vjGm9A6dZR7z.png)
+
+### 题解
+本题要考虑j>i的下标j的情况，则可以从右向左遍历数组，这样当遍历到下标i时下标j及j右侧已经处理过了，必然可以拿到一些信息。考虑下标j，对每个下标j如果其右侧已经遍历过，则此时必然已知一个下标k使得k是大于j的价格小于等于j的最小下标，则对于i，如果j不满足条件，那么价格大于j的当然同样不满足条件，我们要找的是价格小于j的在j右侧的下标，则此时下标k正满足条件。如果k的价格仍不满足条件，则同样在遍历k时已知一个p满足题目条件，再继续找到p，如此链式查找直到找到一个数字的结果的下标就是其自身说明没有满足条件的数字，直接使i的价格为其自身。若找到满足条件的则设为满足条件的价格。
+
+设定两个数组，一个用来保存找到的满足条件的打折扣的数字下标，另一个保存当前下标是否能打折扣。最终遍历数组，对于能打折扣的数字，减去其折扣值。
+
+### 代码
+```cpp 
+class Solution {
+public:
+    vector<int> finalPrices(vector<int>& prices) {
+        int n = prices.size();
+        vector<int> targetindex(n,0);
+        vector<bool> discount(n,false);
+        for(int i=prices.size()-1;i>=0;i--){
+            int nextindex=i+1;
+            if(nextindex == n){
+                targetindex[i] = i;
+                continue;
+            }
+            while(nextindex < n){
+                if(prices[nextindex] > prices[i]){
+                    if(nextindex == targetindex[nextindex]){
+                        targetindex[i] = i;
+                        break;
+                    }else{
+                        nextindex = targetindex[nextindex];
+                    }
+                }else{
+                    targetindex[i] = nextindex;
+                    discount[i] = true;
+                    break;
+                }
+            }
+        }
+        for(int i=0;i<n;i++){
+            if(discount[i]){
+                prices[i] = prices[i]-prices[targetindex[i]];
+            }
+        }
+        return prices;
+    }
+};
+```
+
+## day286 2024-12-19
+### 769. Max Chunks To Make Sorted 
+You are given an integer array arr of length n that represents a permutation of the integers in the range [0, n - 1].
+
+We split arr into some number of chunks (i.e., partitions), and individually sort each chunk. After concatenating them, the result should equal the sorted array.
+
+Return the largest number of chunks we can make to sort the array. 
+
+![1219QG0PhBWCU2Zr](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1219QG0PhBWCU2Zr.png)
+
+### 题解
+本题若要在分块后将块内排序，使得每个块内有序后整体自然有序，则假设块i之前的所有块包含的数字个数为k，则块i必须包含从k+1到出现的块内最大值的所有数字（如果第一个出现的数字是k+3，就要包含k+1~k+3，如果第一个出现的就是k+1，则只包含一个k+1即可）。这样才能保证块内排序后不会出现后面有数字小于块内最大值从而使整体不满足有序这样的问题。则用一个数字统计当前最大值m之前已经出现的数字个数，当数字个数达到m-1时，从上一块结尾开始到当前数字就可以被分为单独的一块。
+此处我们并不需要知道每个块都有哪些数字，只要已经出现了当前最大值之前的全部数字，我们就知道前面的数字一定可以排列成有序的，否则后面还可能出现更小的数字使得整体不满足有序，因此可以排列成有序的时候就可以分为单独的一块。如果数组本身就是有序的，那么按照我们的算法，对每个数字，遍历到该数字时小于该数字的全部数字都已经出现了，则一定可以排列成有序的，因此这个数字本身就可以单独分为一块。
+
+### 代码
+```cpp 
+class Solution {
+public:
+    int maxChunksToSorted(vector<int>& arr) {
+        int count = -1;
+        int result = 0;
+        int maxnum = -1;
+        for(const int& num : arr){
+            maxnum = max(num,maxnum);
+            if (count == maxnum-1){
+                result++;
+            }
+            count++;
+        }
+        return result;
+    }
+};
+```
+## day287 2024-12-20
+### 2415. Reverse Odd Levels of Binary Tree 
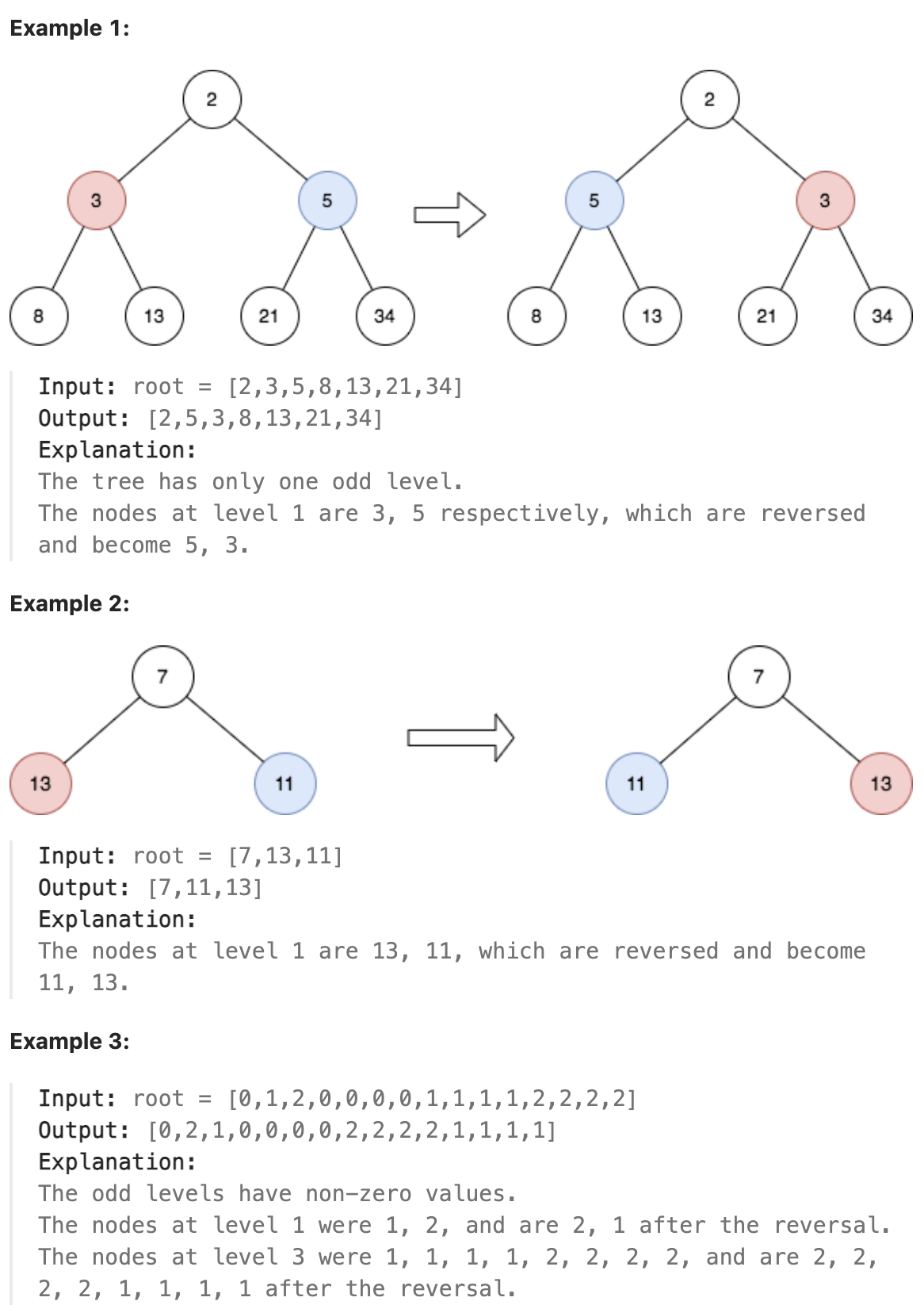
+Given the root of a perfect binary tree, reverse the node values at each odd level of the tree.
+
+For example, suppose the node values at level 3 are [2,1,3,4,7,11,29,18], then it should become [18,29,11,7,4,3,1,2].
+Return the root of the reversed tree.
+
+A binary tree is perfect if all parent nodes have two children and all leaves are on the same level.
+
+The level of a node is the number of edges along the path between it and the root node. 
+
+![1220F7U3F1wDq3QW](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1220F7U3F1wDq3QW.png)
+
+### 题解
+本题可使用层序遍历，用一个变量记录当前访问的层级，对于奇数层将该层的所有节点指针保存在数组中，再通过对首尾指针指向的节点值进行交换并不断移动指针直到到达数组的中间位置正好将所有的值交换完毕，完成了该层节点的值的逆序。
+
+### 代码
+```cpp 
+class Solution {
+public:
+    TreeNode* reverseOddLevels(TreeNode* root) {
+        if (!root) return root;
+        
+        queue<TreeNode*> q;
+        q.push(root);
+        int level = 0;
+        
+        while (!q.empty()) {
+            int size = q.size();
+            vector<TreeNode*> nodes;
+            
+            for (int i = 0; i < size; i++) {
+                TreeNode* curr = q.front();
+                q.pop();
+                
+                if (curr->left) {
+                    q.push(curr->left);
+                    q.push(curr->right);
+                }
+                
+                if (level % 2 == 1) {
+                    nodes.push_back(curr);
+                }
+            }
+            
+            // 对奇数层进行首尾交换
+            if (level % 2 == 1) {
+                int left = 0, right = nodes.size() - 1;
+                while (left < right) {
+                    swap(nodes[left]->val, nodes[right]->val);
+                    left++;
+                    right--;
+                }
+            }
+            
+            level++;
+        }
+        
+        return root;
+    }
+};
+```
+## day288 2024-12-21
+### 2872. Maximum Number of K-Divisible Components 
+There is an undirected tree with n nodes labeled from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
+
+You are also given a 0-indexed integer array values of length n, where values[i] is the value associated with the ith node, and an integer k.
+
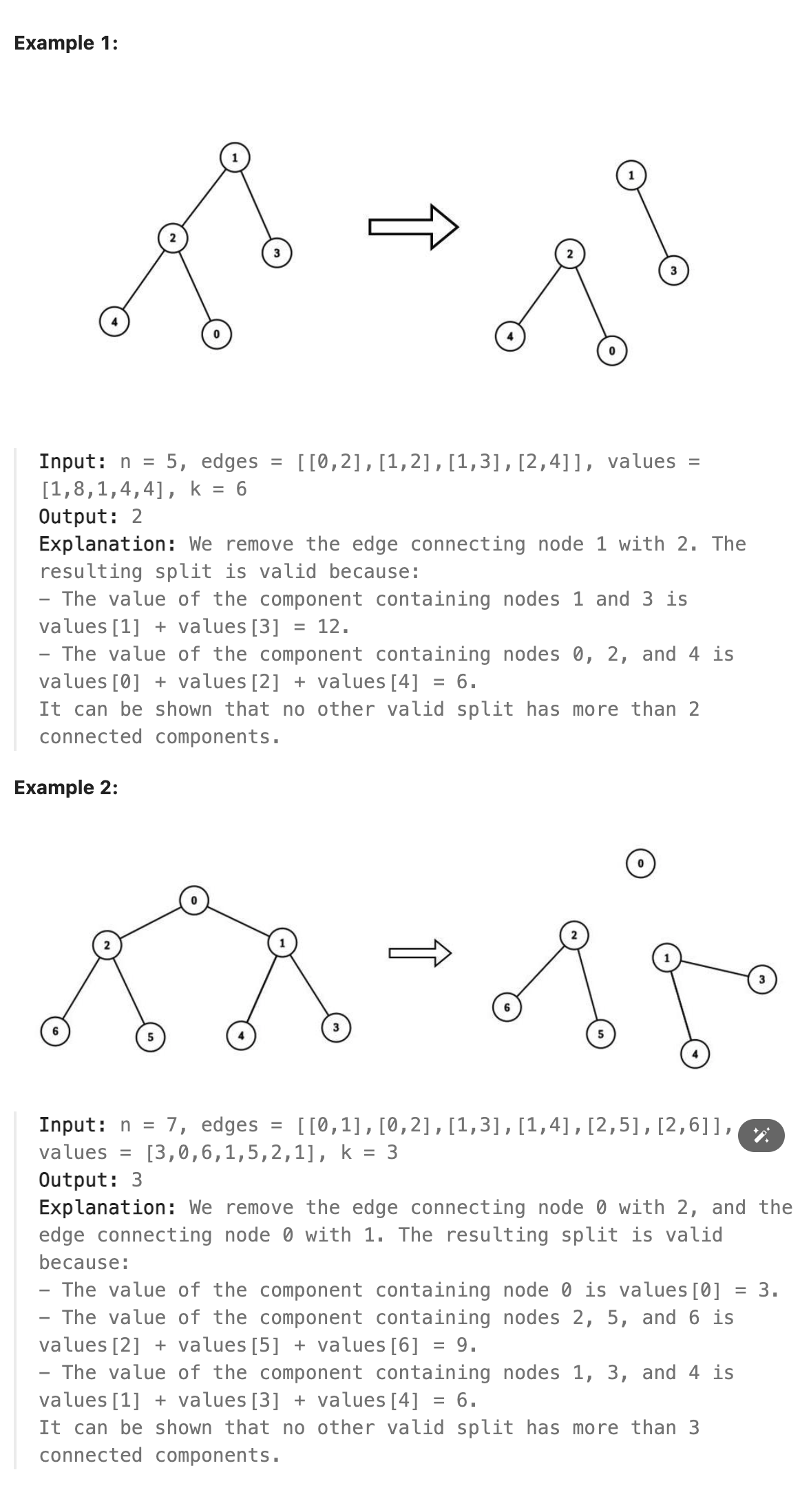
+A valid split of the tree is obtained by removing any set of edges, possibly empty, from the tree such that the resulting components all have values that are divisible by k, where the value of a connected component is the sum of the values of its nodes.
+
+Return the maximum number of components in any valid split. 
+
+![1221gSmFhuhmVag9](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1221gSmFhuhmVag9.png)
+
+### 题解
+题目中说明了给定的数据可以构成一棵无向树，无向树可以选择任意一个节点作为根节点展开，任意选择根节点的情况下无向树未必是一棵二叉树，但一定不存在环。
+
+考虑在任意确定了根节点后，如何寻找满足条件的连通分量。可以从根开始向下，在找到一个连通分量后就删掉这个连通分量，但这样做会存在无向树的剩余部分可能无法构成满足条件的连通分量的问题，如仅有三个节点，节点值分别为6，2，4且值为6的节点与另外两个节点相连，如果k为6且选定了节点值为6的节点作为根节点，那么如果从根开始寻找满足条件的连通分量，6自身就满足条件，此时应该将根节点单独作为一个连通分量，将其与其他两个节点相连的边删去，但这样得到单独的4和单独的2都不满足条件。因此若从选定的根开始向下探索，则由于删掉一个父节点会使得两个子节点被迫分离开，影响了这两个子节点与其他节点构成连通分量。因此这种方法会导致出现不满足条件的连通分量。
+
+但自底向上则不会出现这个问题，我们可以发现，在从底向上寻找满足条件的连通分量的时候，如果找到了一个满足条件的连通分量，这个连通分量与树的其余部分仅会有一条边相连，因此删掉这个连通分量仅需要删掉这一条边即可，这样不会影响树的其余部分继续构成连通分量。没有破坏其余节点之间的相连性。而上面说的从根向下则破坏了原本的两个节点之间的相连性。
+
+理解这一点后，实现时任意选定一个根节点，使用dfs一直遍历到树的最底部，对于dfs自身，递归调用dfs遍历当前节点的所有子树并得到返回值，将返回值和当前节点的值相加，若能被k整除，则将连通分量总数加一并返回0，若不能则返回相加得到的和。递归的退出状态为，当节点没有子节点时，若能被k整除，则同样将总数加一返回0，不能直接返回节点的值。这样通过贪心，每次得到一个有效的连通分量就将其分离开，最终得到了个数最多的连通分量。
+
+### 代码
+```cpp 
+class Solution {
+public:
+    vector<vector<int>> adj; 
+    vector<bool> visited;    
+    vector<int> nodeValues;  
+    int divisor;            
+    int result;             
+
+   
+    long long dfs(int node) {
+        visited[node] = true;
+        long long currentSum = nodeValues[node];  
+
+        for (int neighbor : adj[node]) {
+            if (!visited[neighbor]) {
+                currentSum += dfs(neighbor);
+            }
+        }
+
+        if (currentSum % divisor == 0) {
+            result++;
+            return 0;  
+        }
+
+        return currentSum;  
+    }
+
+    int maxKDivisibleComponents(int n, vector<vector<int>>& edges, vector<int>& values, int k) {
+        adj.resize(n);
+        visited.resize(n, false);
+        nodeValues = values;
+        divisor = k;
+        result = 0;
+
+        for (const auto& edge : edges) {
+            adj[edge[0]].push_back(edge[1]);
+            adj[edge[1]].push_back(edge[0]);
+        }
+
+        // 从节点0开始遍历 
+        dfs(0);
+
+        return result;
+    }
+};
+```
+## day289 2024-12-22
+### 2940. Find Building Where Alice and Bob Can Meet 
+You are given a 0-indexed array heights of positive integers, where heights[i] represents the height of the ith building.
+
+If a person is in building i, they can move to any other building j if and only if i < j and heights[i] < heights[j].
+
+You are also given another array queries where queries[i] = [ai, bi]. On the ith query, Alice is in building ai while Bob is in building bi.
+
+Return an array ans where ans[i] is the index of the leftmost building where Alice and Bob can meet on the ith query. If Alice and Bob cannot move to a common building on query i, set ans[i] to -1.
+
+![1222i3wwqUMS3GRh](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1222i3wwqUMS3GRh.png)
+
+### 题解
+本题考虑Alice和Bob能相遇的情况，Alice和Bob都可以移动到自己初始所处的建筑i的右侧比所处建筑高的建筑，那么无论Alice和Bob谁在右侧，此处假设Alice在左，Bob在右，假如Bob所处的建筑高度已经比Alice高，那么二者直接移动到Bob所处的建筑即满足条件。若Bob所处的建筑不如Alice的高，那么二者需要移动到Bob右侧第一座比Alice所处建筑高度高的位置（这个建筑当然也满足比Bob高，因此Bob也可以移动到此处）。由此可以发现，最关键的就是每个位置的右侧所有比该位置高的建筑的下标和高度。
+
+可以将每个位置右侧所有比该位置高度高的下标和高度全部保存下来，但这样会将同一个建筑重复保存很多遍。是否有更高效的方法能获取到某个建筑右侧所有比该建筑高的全部建筑呢，我们发现其实只需要保存每个位置处右侧比该位置高的第一个建筑的下标就可以了，随后通过链式遍历，就可以得到全部的位置右侧单调增的建筑下标。
+
+这样做在遍历的时候会忽略掉一些建筑，如对于5，4，6这样的建筑高度。如果当前建筑高度为3，那么在链式遍历的时候只会遍历5，6不会遍历4，但这对结果并无影响，因为我们最终需要的是能满足在两个人右侧的比两个人建筑都高的第一个建筑的下标，如果5不满足条件，那么当然4也不满足条件，而即使4也满足条件，那么因为5在4的左侧，所以优先选择5，由此只保存每个位置右侧第一个比当前位置高的下标就足够了。这也是为什么后面可以使用单调栈。
+
+则本题先通过逆序遍历数组并构造单调栈的形式确定每个位置右侧第一个高于该位置的建筑下标并保存。再遍历query，根据query先确定谁在右侧，并判断在右侧的高度是否更高，如果更高则直接将右侧下标作为结果，如果不是则开始链式遍历比右侧建筑高的全部建筑并将高于左侧建筑高度的第一个建筑的下标作为结果。
+
+思路是正确的，但对于少数几个例子会超时，因此需要再继续优化一下，可以发现在构造单调栈的过程中完全可以一边构造一边找出结果，只需要先将每个位置对应的所有query（即query中靠右的下标为该query对应的查询位置）都保存下来，这样就可以在逆序构造单调栈的过程中，对该位置对应的所有query，在单调栈中查找满足该query的结果，查找结果可以使用二分法来加速查找，这样一边查找一边将该位置的建筑高度用于继续构造单调栈。这样在构造单调栈的同时实现了对结果的查找。
+
+### 代码
+```cpp 
+class Solution {
+public:
+    vector<int> leftmostBuildingQueries(vector<int>& heights, vector<vector<int>>& queries) {
+        int n = heights.size();
+        int m = queries.size();
+        vector<int> ans(m, -1);
+        
+        // 将查询按右端点分组
+        vector<vector<pair<int, int>>> queryGroups(n);  // {左端点, 查询索引}
+        for (int i = 0; i < m; i++) {
+            int a = queries[i][0], b = queries[i][1];
+            if (a > b) swap(a, b);
+            // 如果是同一建筑或右边建筑更高，直接得到结果
+            if (a == b || heights[b] > heights[a]) {
+                ans[i] = b;
+                continue;
+            }
+            queryGroups[b].push_back({a, i});
+        }
+        
+        vector<pair<int, int>> stack;  // {高度, 下标}
+        
+        // 从右向左构建单调递减栈并处理查询
+        for (int i = n - 1; i >= 0; i--) {
+            // 处理当前位置的所有查询
+            for (auto& query : queryGroups[i]) {
+                int left = query.first;
+                int queryIndex = query.second;
+                int targetHeight = max(heights[left], heights[i]);
+                
+                int l = 0, r = stack.size() - 1;
+                int pos = -1;
+                while (l <= r) {
+                    int mid = l + (r - l) / 2;
+                    if (stack[mid].first > targetHeight) {
+                        pos = mid;
+                        l = mid + 1;
+                    } else {
+                        r = mid - 1;
+                    }
+                }
+                
+                if (pos != -1) {
+                    ans[queryIndex] = stack[pos].second;
+                }
+            }
+            
+            // 维护单调递减栈
+            while (!stack.empty() && stack.back().first <= heights[i]) {
+                stack.pop_back();
+            }
+            stack.push_back({heights[i], i});
+        }
+        
+        return ans;
+    }
+};
+
+```
+## day290 2024-12-23
+### 2471. Minimum Number of Operations to Sort a Binary Tree by Level 
+You are given the root of a binary tree with unique values.
+
+In one operation, you can choose any two nodes at the same level and swap their values.
+
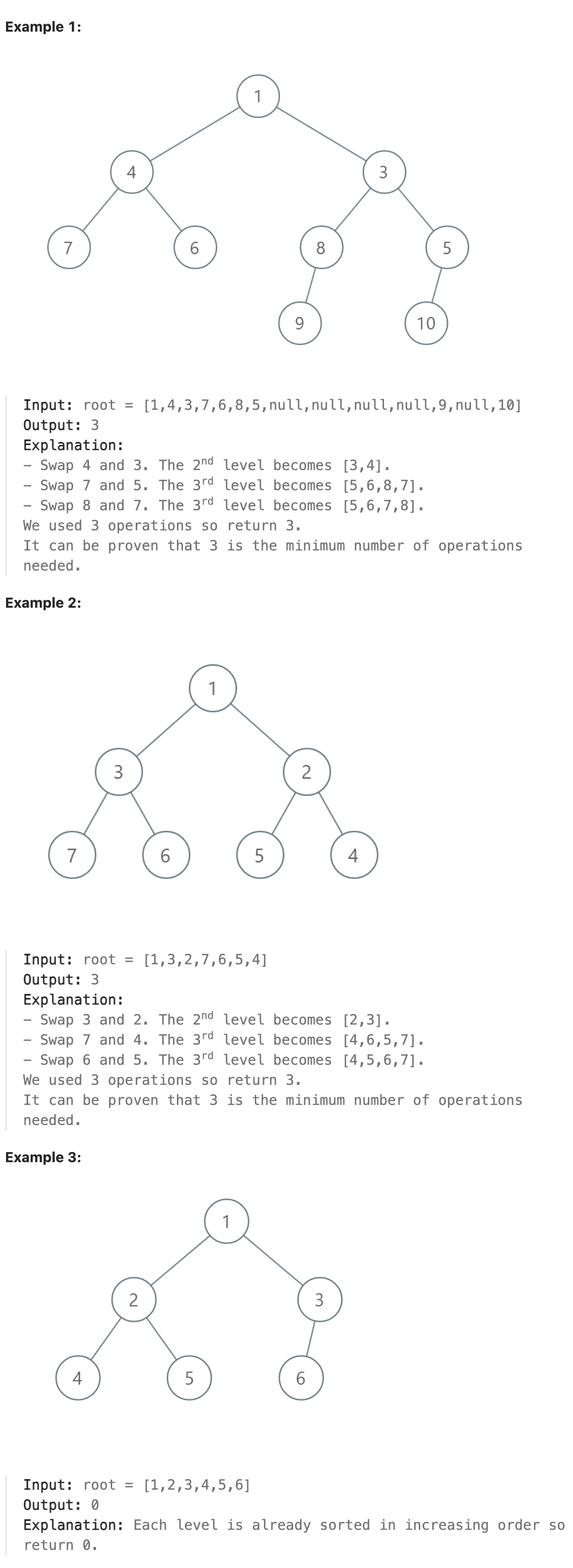
+Return the minimum number of operations needed to make the values at each level sorted in a strictly increasing order.
+
+The level of a node is the number of edges along the path between it and the root node. 
+
+![1223hMOXrD0HsyuY](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1223hMOXrD0HsyuY.png)
+
+### 题解
+本题可以通过bfs来对二叉树按层进行处理，对二叉树每一层，将该层的全部数字保存下来，因为二叉树中所有节点的值均不重复，因此可以构造一个大数组，数组下标为节点的值，数组的值为该数字在当前层数字中的下标位置（设整个大数组为tree，则例如在第一层中数字6是从左到右第二个，那么tree\[6\]=1，在前面的题目中多次使用过这种思路)。再将该层的原始数组排序，遍历有序数组，根据每个位置应该放置的数字将当前位置的数字和目标数字交换。并将在大数组中保存的数字对应的下标做相应交换调整。如果需要交换数字则给结果加1，不需要则继续向后遍历。
+
+### 代码
+```cpp 
+class Solution {
+public:
+    vector<int> pos;
+    Solution() : pos(100001) { }  // 在构造函数中初始化
+    int minimumOperations(TreeNode* root) {
+        if (!root) return 0;
+        
+        int result = 0;
+        queue<TreeNode*> q;
+        q.push(root);
+        
+        while (!q.empty()) {
+            int size = q.size();
+            vector<int> level; 
+            
+            // 获取当前层的所有节点值
+            for (int i = 0; i < size; i++) {
+                TreeNode* node = q.front();
+                q.pop();
+                level.push_back(node->val);
+                
+                if (node->left) q.push(node->left);
+                if (node->right) q.push(node->right);
+            }
+            
+            result += countSwaps(level);
+        }
+        
+        return result;
+    }
+    
+private:
+    int countSwaps(vector<int>& arr) {
+        int n = arr.size();
+        
+        for (int i = 0; i < n; i++) {
+            pos[arr[i]] = i;
+        }
+        
+        vector<int> sorted = arr;
+        sort(sorted.begin(), sorted.end());
+        
+        int swaps = 0;
+        for (int i = 0; i < n; i++) {
+            if (arr[i] != sorted[i]) {
+                swaps++;
+                
+                int oldVal = arr[i];
+                int newVal = sorted[i];
+                
+                arr[i] = newVal;
+                arr[pos[newVal]] = oldVal;
+                
+                int temp = pos[oldVal];
+                pos[oldVal] = pos[newVal];
+                pos[newVal] = temp;
+            }
+        }
+        
+        return swaps;
+    }
+};
+```
+## day291 2024-12-24
+### 3203. Find Minimum Diameter After Merging Two Trees 
+There exist two undirected trees with n and m nodes, numbered from 0 to n - 1 and from 0 to m - 1, respectively. You are given two 2D integer arrays edges1 and edges2 of lengths n - 1 and m - 1, respectively, where edges1[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the first tree and edges2[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the second tree.
+
+You must connect one node from the first tree with another node from the second tree with an edge.
+
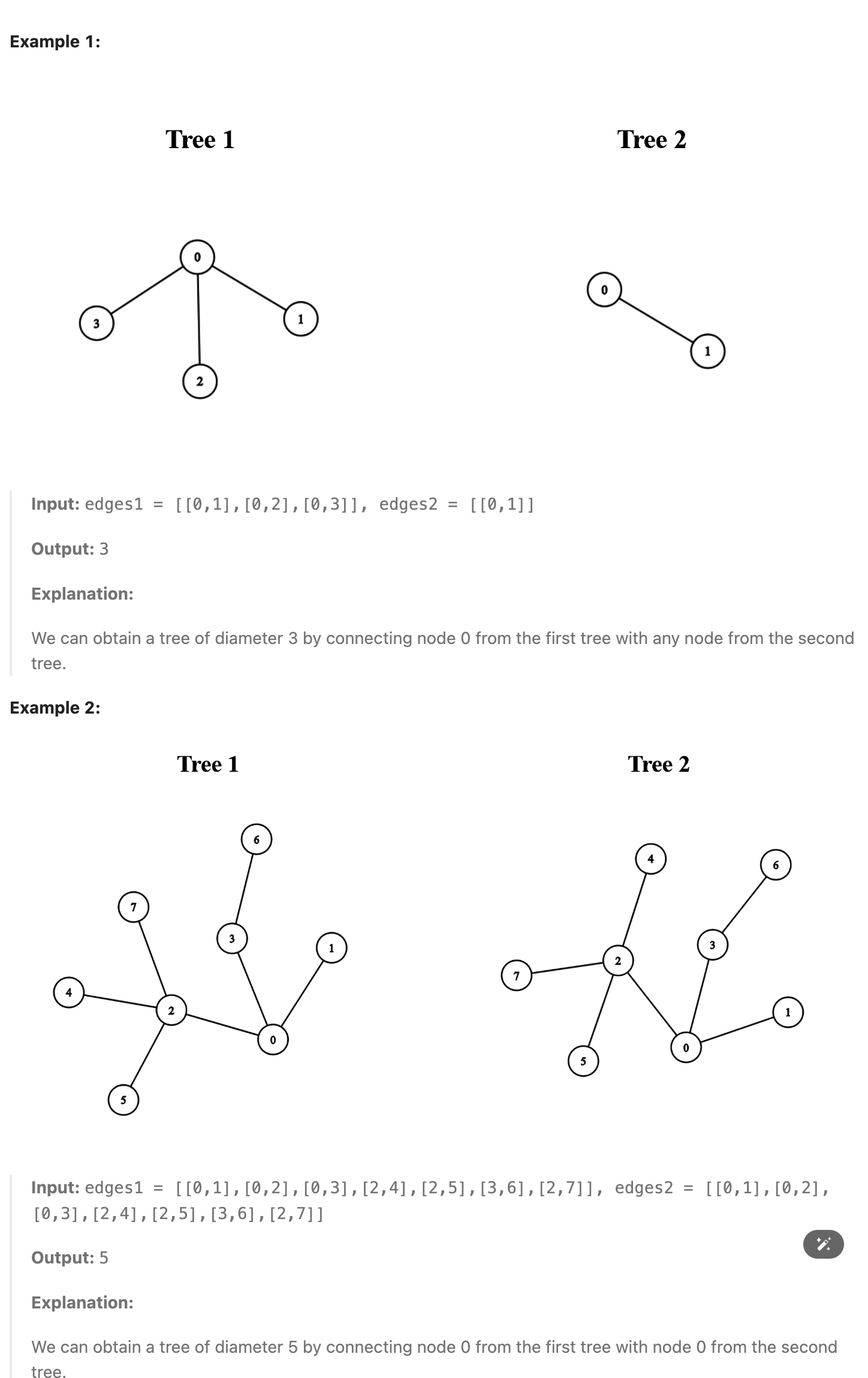
+Return the minimum possible diameter of the resulting tree.
+
+The diameter of a tree is the length of the longest path between any two nodes in the tree. 
+
+![1224k4jcxOAzr8A0](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1224k4jcxOAzr8A0.png)
+
+### 题解
+本题的总体思路其实比较容易想到，要找到的是两棵树上的两个节点，使得将这两个节点连接后得到的新树的直径最短。原始的两棵树是固定的，若要在连接后直径最短，则用于连接的节点在原来的树上到其他任何一个节点距离的最大值应该尽可能小，问题在于这样的节点应该如何确定。
+
+树的直径是树中任意两节点之间最长的简单路径，直径是整棵树中最长的路径，那么要想使得最大值尽可能小，就应该找直径的中点，对于直径是偶数，中点只有一个，直径是奇数则任选两个中点中的一个即可。其他节点都会存在到直径的两个端点的更长距离，因为其他节点到端点都要先经过中点，再到端点。
+
+确定树的直径使用两次dfs即可，第一次dfs确定直径的一个端点，第二次dfs就可以确定直径的长度，对于奇数，将直径长度除以二取上整，偶数则直接除以二。将两棵树的直径长度除以二后相加即得最终结果。
+
+真的得到最终结果了吗，并没有，还要考虑这样的情况，即一棵树的直径非常短，则两棵树的直径的1/2相加后的结果小于其中一棵树自身的直径，此时由于是通过节点将两棵树相连构成一棵树，因此每棵树自身当然是包含在树中的，因此要取树自身的直径和相连后通过两棵树的中间节点计算出来的直径的最大值才能得到最终的正确答案。
+
+### 代码
+```cpp 
+class Solution {
+private:
+    void buildGraph(vector<vector<int>>& edges, vector<vector<int>>& graph) {
+        for (const auto& edge : edges) {
+            graph[edge[0]].push_back(edge[1]);
+            graph[edge[1]].push_back(edge[0]);
+        }
+    }
+    
+    void dfs1(int node, int parent, int dist, int& maxDist, int& farthestNode, vector<vector<int>>& graph) {
+        if (dist > maxDist) {
+            maxDist = dist;
+            farthestNode = node;
+        }
+        
+        for (int next : graph[node]) {
+            if (next != parent) {
+                dfs1(next, node, dist + 1, maxDist, farthestNode, graph);
+            }
+        }
+    }
+    
+    void dfs2(int node, int parent, int dist, int& maxDist, vector<vector<int>>& graph) {
+        maxDist = max(maxDist, dist);
+        
+        for (int next : graph[node]) {
+            if (next != parent) {
+                dfs2(next, node, dist + 1, maxDist, graph);
+            }
+        }
+    }
+    
+    int getDiameter(vector<vector<int>>& edges, int n) {
+        vector<vector<int>> graph(n);
+        buildGraph(edges, graph);
+        
+        // 第一次DFS找最远点
+        int maxDist = 0, farthestNode = 0;
+        dfs1(0, -1, 0, maxDist, farthestNode, graph);
+        
+        // 第二次DFS找直径
+        maxDist = 0;
+        dfs2(farthestNode, -1, 0, maxDist, graph);
+        
+        return maxDist;
+    }
+    
+public:
+    int minimumDiameterAfterMerge(vector<vector<int>>& edges1, vector<vector<int>>& edges2) {
+        int n = edges1.size() + 1;
+        int m = edges2.size() + 1;
+        
+        // 分别计算两棵树的直径
+        int diameter1 = getDiameter(edges1, n);
+        int diameter2 = getDiameter(edges2, m);
+
+        int maxdia = max(diameter1,diameter2);
+
+        
+        return max(maxdia,(diameter1 + 1) / 2 + (diameter2 + 1) / 2 + 1);
+    }
+};
+```
+
+## day292 2024-12-25
+### 515. Find Largest Value in Each Tree Row 
+
+Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed).
+
+![1225bPdlxmAvYcFk](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1225bPdlxmAvYcFk.png)
+
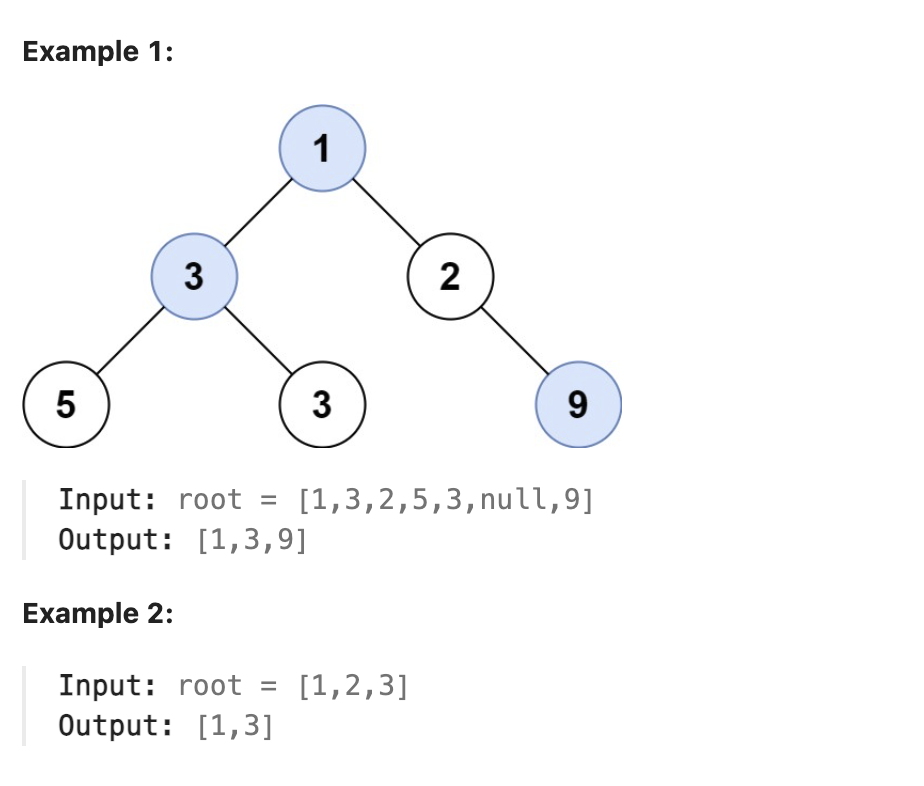
+### 题解
+本题是比较常规的遍历二叉树的题目，使用BFS进行层序遍历，并且在每一层遍历时保存当前层的最大值直到遍历完该层，将最大值放入结果数组中即可。
+
+### 代码
+```cpp 
+
+/**
+ * Definition for a binary tree node.
+ * struct TreeNode {
+ *     int val;
+ *     TreeNode *left;
+ *     TreeNode *right;
+ *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
+ *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
+ *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
+ * };
+ */
+class Solution {
+public:
+    vector<int> largestValues(TreeNode* root) {
+        if (!root) return {};
+        
+        vector<int> result;
+        queue<TreeNode*> q;
+        q.push(root);
+        
+        while (!q.empty()) {
+            int levelSize = q.size();
+            int maxVal = INT_MIN;  // 初始化当前层的最大值
+            
+            // 遍历当前层的所有节点
+            for (int i = 0; i < levelSize; i++) {
+                TreeNode* node = q.front();
+                q.pop();
+                
+                // 更新当前层的最大值
+                maxVal = max(maxVal, node->val);
+                
+                // 将下一层的节点加入队列
+                if (node->left) {
+                    q.push(node->left);
+                }
+                if (node->right) {
+                    q.push(node->right);
+                }
+            }
+            
+            // 将当前层的最大值加入结果数组
+            result.push_back(maxVal);
+        }
+        
+        return result;
+    }
+};
+```
+## day293 2024-12-26
+### 494. Target Sum 
+You are given an integer array nums and an integer target.
+
+You want to build an expression out of nums by adding one of the symbols '+' and '-' before each integer in nums and then concatenate all the integers.
+
+For example, if nums = [2, 1], you can add a '+' before 2 and a '-' before 1 and concatenate them to build the expression "+2-1".
+Return the number of different expressions that you can build, which evaluates to target. 
+
+![1226B0EYGDIq0D8o](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1226B0EYGDIq0D8o.png)
+
+### 题解
+本题是一道很经典的记忆化问题，考虑计算数字和的过程，每个数字都有加或者减两种选择，那么n个数字就有2^n种可能，但可以注意到在数字加和过程中的两个特点。第一个特点是通过不同的加减和组合方式有可能能得出相同的结果。最简单的例子，如三个1，可以通过+1+1-1的方式得到和1，也可以通过+1-1+1的方式得到和1。第二个特点是从某个下标开始到数组最后能得到的全部可能结果仅与到这个下标为止已经得到的和有关，而与得到这个和的具体路径无关。例如前面已经得到了和为6，那么后面就在得到的和6的基础上进行加减操作，具体6是如何来的并不重要。
+
+那么我们就可以保存到某个下标m前面所有数字的全部可能的和，每个和对应的通过加减后面的数字直到数组末尾最终得到target的可能路径的个数。通过递归得出第一个数字到数组末尾得到target的可能的路径个数。
+
+递归过程中，对当前遍历到的数字，有两条路径，可以将当前数字加上之前数字的和再向后递归，也可以将之前的和减去当前数字作为新的和向后递归，如果当前数字对应的前面所有数字的和在之前的递归路径中已经被计算过，则可直接返回该和对应的最终能得到target的路径个数。
+
+### 代码
+```cpp 
+
+class Solution {
+private:
+    vector<vector<int>> dp;
+    int offset = 1000; 
+    
+    int dfs(vector<int>& nums, int target, int index, int sum) {
+        if (index == nums.size()) {
+            return sum == target ? 1 : 0;
+        }
+        
+        // 如果当前状态已计算过，直接返回
+        if (dp[index][sum + offset] != -1) {
+            return dp[index][sum + offset];
+        }
+        
+        // 递归计算两种选择：加号和减号
+        dp[index][sum + offset] = dfs(nums, target, index + 1, sum + nums[index]) + dfs(nums, target, index + 1, sum - nums[index]);
+        
+        return dp[index][sum + offset];
+    }
+    
+public:
+    int findTargetSumWays(vector<int>& nums, int target) {
+        dp.assign(nums.size(), vector<int>(2001, -1));
+        return dfs(nums, target, 0, 0);
+    }
+};
+```
+## day294 2024-12-27
+### 1014. Best Sightseeing Pair 
+You are given an integer array values where values[i] represents the value of the ith sightseeing spot. Two sightseeing spots i and j have a distance j - i between them.
+
+The score of a pair (i < j) of sightseeing spots is values[i] + values[j] + i - j: the sum of the values of the sightseeing spots, minus the distance between them.
+
+Return the maximum score of a pair of sightseeing spots. 
+
+![1227W5w7glO9LWAG](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1227W5w7glO9LWAG.png)
+
+### 题解
+本题涉及两个变化因素，一个是数字本身的值，另一个就是数字之间的距离，在遍历数组的过程中，可以发现对于某个固定位置的数字，距离会自然发生递增或者递减的变化。但值是不确定的，对于有两个变化因素的问题，我们一般固定一个因素，再按照某种规律去改变另一个因素，这样就将难以处理的变化问题变成了只需考虑一个有规律的因素的问题。很多多因素问题就是通过对其中某些因素进行限制，或者固定，最终只剩余一个因素变化，从而得到O(n)的时间复杂度，或者说要想得到O(n)的复杂度，就要想办法构建只有一个变化因素的情况，这样只需处理一个因素，就可以通过一次遍历来解决。本题中，在向后遍历数组的过程中，前面的数字距离当前数字的距离是自然的递增的，每向后遍历一个数字距离加一，假设当前的下标为m，假设之前的某个数字的下标为i，则我们可以考虑这样一个量，即数字i对于m的真实价值，设为values[i]+i-m。即i自身的值减去i和m之间的距离。此处相当于固定了两个加和的数字中后面的数字为m，只需考虑前面数字中如何取得最大值即可。我们在遍历的时候保存到当前位置的数字的真实价值的最大值，用当前数字的值与这个最大值相加即得当前数字和前面的数字能够取得的数对的最大值。
+
+每当遍历到一个新数字时，我们将之前的最大真实值减一和当前数字的值做比较并更新最大真实值，这样计算的是对于后面的数字来说，前面的数字中的最大真实值，如此只需遍历一遍数组即可得数组中数对的最大值。
+
+### 代码
+```cpp 
+class Solution {
+public:
+    int maxScoreSightseeingPair(vector<int>& values) {
+        int maxrealvalue = values[0];
+        int maxresult = 0;
+        for(int i=1;i<values.size();i++){
+            maxrealvalue--;
+            maxresult = max(maxresult, maxrealvalue+values[i]);
+            maxrealvalue = max(maxrealvalue, values[i]);
+        }
+        return maxresult;
+    }
+};
+```