Logic/hugo
1
0
Fork 0
mirror of https://gitlab.com/game-loader/hugo.git synced 2025-04-20 05:52:07 +08:00
Code Issues Actions Packages Projects Releases Wiki Activity

leetcode update

Browse Source
This commit is contained in:
gameloader 2024-12-05 08:42:23 +08:00
parent 386591c939
commit 61e8937aac
1 changed files with 232 additions and 0 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

232
content/posts/leetcode.md
View File

@ -18492,3 +18492,235 @@ private:
} }
}; };
``` ```
## day265 2024-11-28
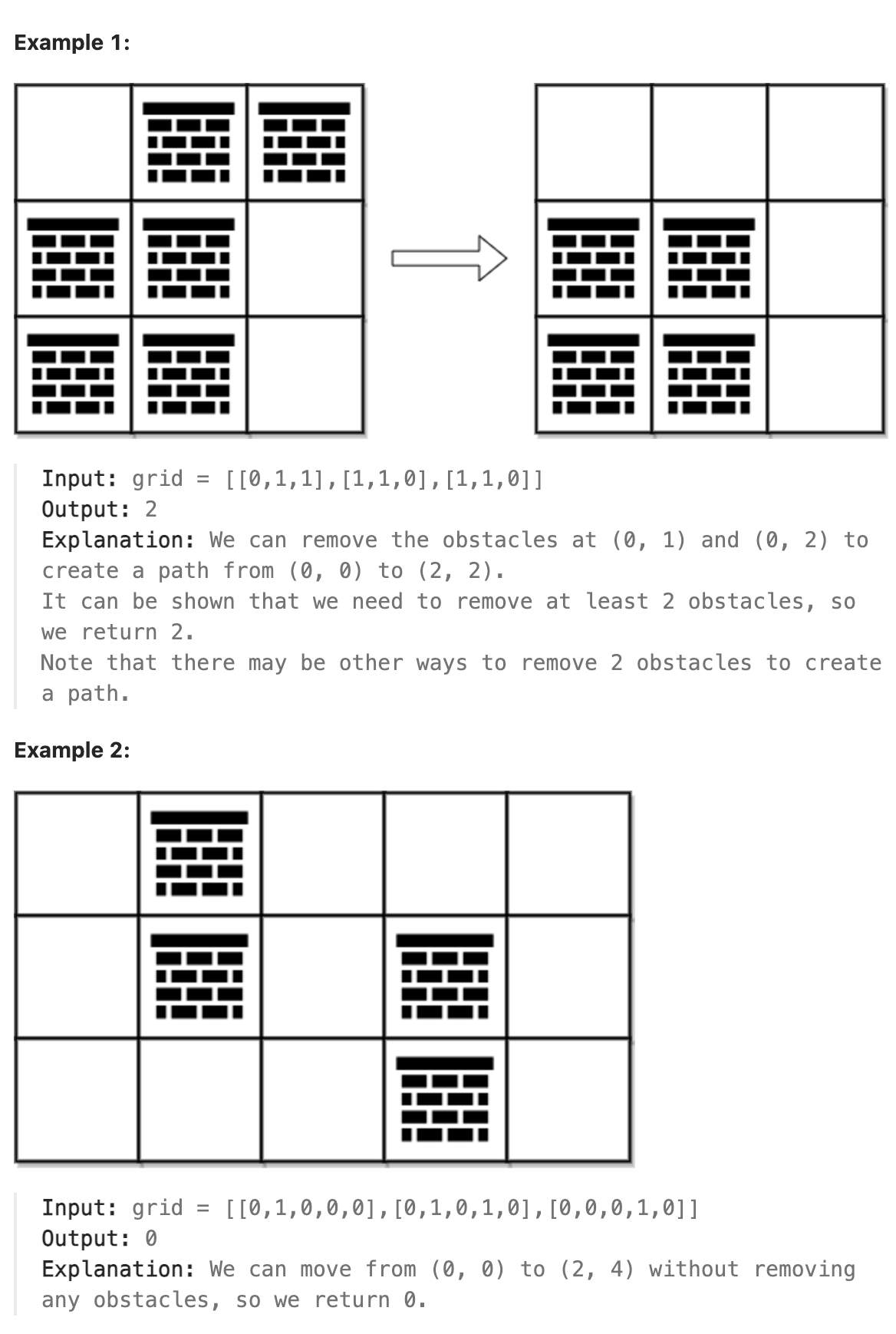
### 2290. Minimum Obstacle Removal to Reach Corner
You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values:
0 represents an empty cell,
1 represents an obstacle that may be removed.
You can move up, down, left, or right from and to an empty cell.
Return the minimum number of obstacles to remove so you can move from the upper left corner (0, 0) to the lower right corner (m - 1, n - 1).
![11288J5wLzndHQBS](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/11288J5wLzndHQBS.png)
### 题解
本题是一道难题，关键在于如何建模寻路的过程，一般提到寻路或者路径规划相关的问题，都会想到这是一个图问题，本题中如何将在数组中寻路转换为在图上寻路，并能得到最小成本就是解题的关键。在图上找到成本最小的路径无异于在图上寻找两个节点之间的最短路径，由于边的权重不存在负值，这就是一道典型的可以用dijistra算法解决的问题。
问题在于如何转换，考虑从任何一个位置出发向四个方向移动，如果遇到墙，想要经过墙就必须要花费移除墙的“成本”。最终要求的是移除最少数量的墙的路径，则每个墙都可以视为要花费1点成本。对于没有墙的位置，移动过去不需要花费成本，则将矩阵中每个位置都视为一个独立的节点，如果某个位置有墙，则向这个位置移动的成本就为1，每个位置都和四个方向的其他位置节点之间存在边，如果移动的成本为1，则边权为1，否则为0，此时就转化成了在图上寻找最短路径的问题，可以使用dijistra算法解决。
### 代码
```cpp
class Solution {
public:
int minimumObstacles(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<int> dx = {-1, 1, 0, 0};
vector<int> dy = {0, 0, -1, 1};
// 优先级队列实现dijistra算法
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
vector<vector<int>> dist(m, vector<int>(n, INT_MAX));
dist[0][0] = grid[0][0];
pq.push({dist[0][0], 0});
while (!pq.empty()) {
auto [cost, pos] = pq.top();
pq.pop();
int x = pos / n;
int y = pos % n;
if (cost > dist[x][y]) continue;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && nx < m && ny >= 0 && ny < n) {
int newCost = cost + grid[nx][ny];
if (newCost < dist[nx][ny]) {
dist[nx][ny] = newCost;
pq.push({newCost, nx * n + ny});
}
}
}
}
return dist[m-1][n-1];
}
};
```
## day266 2024-11-29
### 2577. Minimum Time to Visit a Cell In a Grid
You are given a m x n matrix grid consisting of non-negative integers where grid[row][col] represents the minimum time required to be able to visit the cell (row, col), which means you can visit the cell (row, col) only when the time you visit it is greater than or equal to grid[row][col].
You are standing in the top-left cell of the matrix in the 0th second, and you must move to any adjacent cell in the four directions: up, down, left, and right. Each move you make takes 1 second.
Return the minimum time required in which you can visit the bottom-right cell of the matrix. If you cannot visit the bottom-right cell, then return -1.
![1129uNi8EoWpGKuf](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1129uNi8EoWpGKuf.png)
### 题解
本题仍可以使用dijistra算法解决，像昨天的问题一样，将每个位置视为节点，只不过将每个位置对应的时间视为到这个节点的总成本，同时因为可以在两个节点间来回移动直到时间足够能移动到下一个节点，则只要能从原始位置通过一个时间间隔移动到相邻的位置就可以通过来回移动直到时间足够能移动到下一个相邻可移动位置。但要注意，在来回移动的时候要想继续向当前位置的下一个相邻位置移动，需要移动偶数次步数，因为奇数次步数会移动回当前位置的前一个位置，偶数才会移动回当前位置。
在最开始，只要能从初始位置移动到相邻位置，后面就可以使用dijistra找到到达右下角的最短路径。
### 代码
```cpp
class Solution {
public:
int minimumTime(vector<vector<int>>& grid) {
// 如果一开始就无法移动，直接返回-1
if (grid[0][1] > 1 && grid[1][0] > 1) return -1;
int m = grid.size(), n = grid[0].size();
vector<vector<int>> dist(m, vector<int>(n, INT_MAX));
dist[0][0] = 0;
vector<pair<int, int>> dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
priority_queue<pair<int, pair<int, int>>,
vector<pair<int, pair<int, int>>>,
greater<>> pq;
pq.push({0, {0, 0}});
while (!pq.empty()) {
auto [time, pos] = pq.top();
auto [x, y] = pos;
pq.pop();
if (time > dist[x][y]) continue;
for (const auto& dir : dirs) {
int nx = x + dir.first;
int ny = y + dir.second;
if (nx >= 0 && nx < m && ny >= 0 && ny < n) {
int nextTime = time + 1;
// 需要等待到满足要求的时间
if (grid[nx][ny] > nextTime) {
// 如果时间差是奇数，需要多等一步
nextTime = grid[nx][ny];
if ((grid[nx][ny] - time) % 2 == 0) {
nextTime++;
}
}
if (nextTime < dist[nx][ny]) {
dist[nx][ny] = nextTime;
pq.push({nextTime, {nx, ny}});
}
}
}
}
return dist[m-1][n-1] == INT_MAX ? -1 : dist[m-1][n-1];
}
};
```
## day267 2024-11-30
### 2097. Valid Arrangement of Pairs
You are given a 0-indexed 2D integer array pairs where pairs[i] = [starti, endi]. An arrangement of pairs is valid if for every index i where 1 <= i < pairs.length, we have endi-1 == starti.
Return any valid arrangement of pairs.
Note: The inputs will be generated such that there exists a valid arrangement of pairs.
![1130P2sjjTCttOLr](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1130P2sjjTCttOLr.png)
### 题解
本题是一道典型的图问题，每一个pair有一个start和end相当于一个有向边的起始和终止节点。而本题即找图中一条可以一次性经过图中全部边且不重复的路径问题，也就是一个欧拉图问题。这种图问题如果不了解相关知识是比较难解的，像在一个欧拉图中寻找欧拉路径的问题当前已经有比较经典的算法，故本题可以使用Hierholzer算法解决。注意本题中要寻找的是欧拉通路而不是欧拉回路。对于欧拉图的简单介绍可以参考
[欧拉图](https://oi-wiki.org/graph/euler/)
我们要思考的是，Hierholzer算法是怎么来的，为什么可以想到这样的算法思路。考虑有向图的情况，在有向图中，若图是欧拉图，则起点
### 代码
```cpp
class Solution {
public:
vector<vector<int>> validArrangement(vector<vector<int>>& pairs) {
unordered_map<int, vector<int>> graph;
unordered_map<int, int> inDegree, outDegree;
for (const auto& pair : pairs) {
int u = pair[0], v = pair[1];
graph[u].push_back(v);
outDegree[u]++;
inDegree[v]++;
}
int start = pairs[0][0];
for (const auto& [node, _] : graph) {
if (outDegree[node] > inDegree[node]) {
start = node;
break;
}
}
deque<int> path;
stack<int> stk;
stk.push(start);
while (!stk.empty()) {
int u = stk.top();
if (graph[u].empty()) {
path.push_front(u);
stk.pop();
} else {
stk.push(graph[u].back());
graph[u].pop_back();
}
}
vector<vector<int>> result;
for (auto it = path.begin(); it != prev(path.end()); ++it) {
result.push_back({*it, *next(it)});
}
return result;
}
};
```
## day268 2024-12-01
### 1346. Check If N and Its Double Exist
Given an array arr of integers, check if there exist two indices i and j such that :
i != j
0 <= i, j < arr.length
arr[i] == 2 * arr[j]
![1201DFIHsnacqzZu](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1201DFIHsnacqzZu.png)
### 题解
本题可以使用集合，在遍历数组的过程中将每个数的2倍和1/2都放入集合中，在继续遍历的过程中一旦碰到了集合中已有的数字就返回true，否则返回false。本题只要求返回是否存在这样的组合不要求返回具体的组合对应的下标，故使用集合记录满足条件的数字即能得到最终结果，若要返回具体的下标，则可以构造结构体将每个数对应的原始下标也保存下来。
### 代码
```cpp
class Solution {
public:
bool checkIfExist(vector<int>& arr) {
set<int> sets;
for(const int& num : arr){
if (sets.find(num) != sets.end()){
return true;
}
if(num % 2 == 0){
sets.insert(num/2);
}
sets.insert(num*2);
}
return false;
}
};
```