leetcode update

content/posts/leetcode.md

@@ -9424,3 +9424,112 @@ func delNodes(root *TreeNode, to_delete []int) []*TreeNode {
     return result
 }
 ```
+
+## day143 2024-07-18
+### 1530. Number of Good Leaf Nodes Pairs 
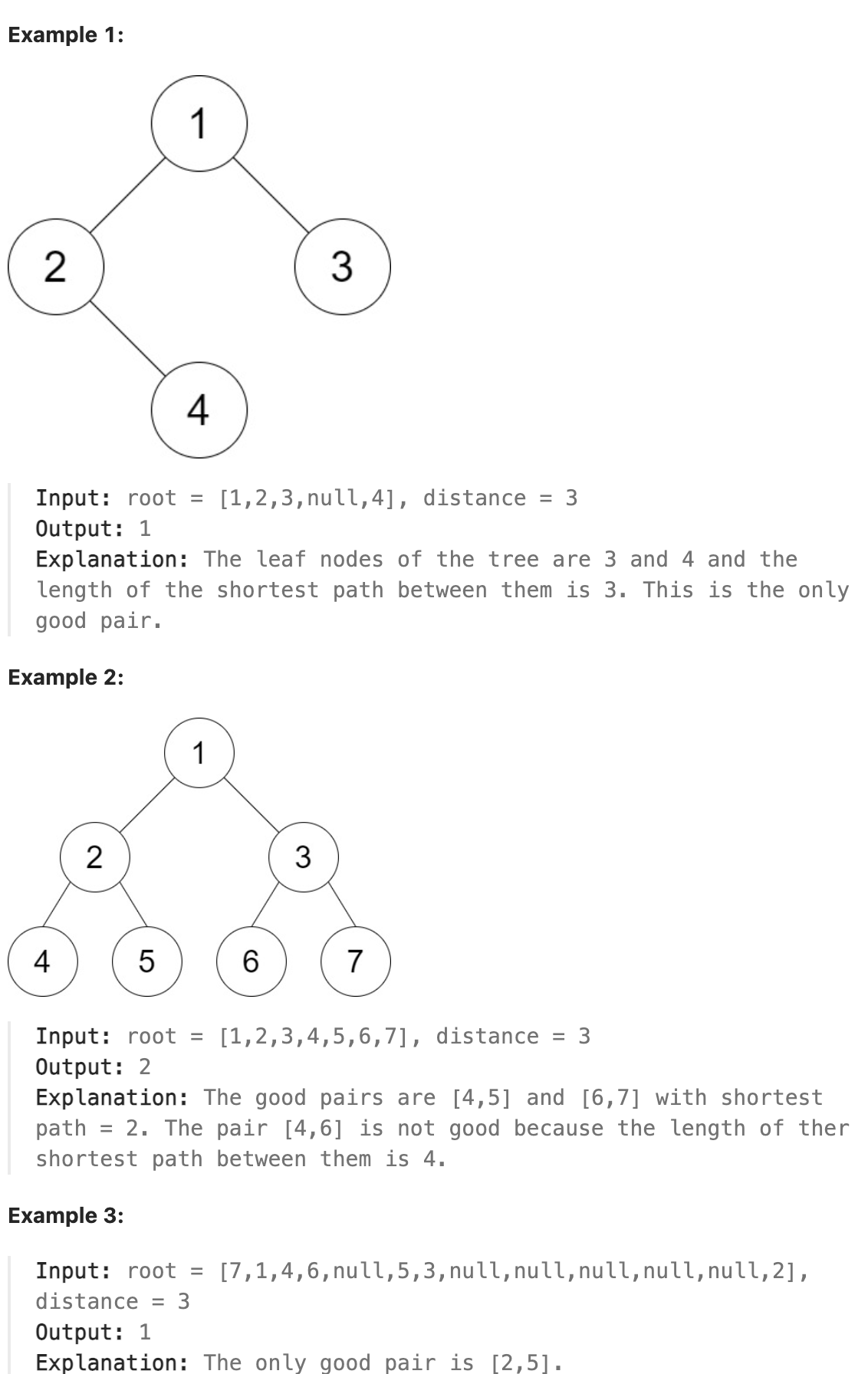
+You are given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.
+
+Return the number of good leaf node pairs in the tree.
+
+![0718DCKotaG6SnQm](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0718DCKotaG6SnQm.png)
+
+### 题解
+考虑对于一个节点来说, 只要知道了到其左子树的所有叶子节点的距离, 和到其右子树的所有叶子节点的距离, 就可以将左子树的所有叶子节点距离和右子树所有叶子节点距离依次加和并与distance比较. 则通过后序遍历, 先遍历左右子树最后将左右子树的叶子节点的距离(数组)返回, 按照上面的思路与distance做比较, 直到遍历完整棵树为止. 这里可以将到叶子节点的最短距离记录下来用于优化, 当左右子树到叶子节点的最小值和已经大于distance时, 其余节点没必要继续进行比较. 直接返回即可.
+
+### 代码
+```go 
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ *     Val int
+ *     Left *TreeNode
+ *     Right *TreeNode
+ * }
+ */
+func countPairs(root *TreeNode, distance int) int {
+    result := 0
+    var dfs func(*TreeNode)([]int, int)
+    dfs = func(root *TreeNode)([]int, int){
+        if root.Left == nil && root.Right == nil{
+            return []int{0},0
+        }
+        leftTree := []int{}
+        leftmin := 0
+        rightTree := []int{}
+        rightmin := 0
+        if root.Left != nil{
+            leftTree, leftmin = dfs(root.Left)
+        }
+        if root.Right != nil{
+            rightTree, rightmin = dfs(root.Right)
+        }
+        minvalue := 2000
+        returnTree := []int{}
+        for _,value := range leftTree{
+            returnTree = append(returnTree, value+1)
+            minvalue = min(minvalue, value+1)
+        }
+        for _,value := range rightTree{
+            returnTree = append(returnTree, value+1)
+            minvalue = min(minvalue, value+1)
+        }
+        if leftmin+rightmin+2 > distance{
+            return returnTree, minvalue
+        }
+        for _,value := range leftTree{
+            for _, value2 := range rightTree{
+                if value+value2+2 <= distance{
+                    result++
+                }
+            }
+        }
+        return returnTree, minvalue
+    }
+    dfs(root)
+    return result
+}
+```
+### 总结
+该种解法的时间复杂度与叶子节点的数量有关(约为节点总数乘以叶子节点数量的平方), 考虑节点总数最多为2的10次方, 则叶子节点最多为2的9次方即512个, 即便是平方的复杂度也在可以接受的范围内.
+
+## day144 2024-07-19
+### 1380. Lucky Numbers in a Matrix 
+Given an m x n matrix of distinct numbers, return all lucky numbers in the matrix in any order.
+
+A lucky number is an element of the matrix such that it is the minimum element in its row and maximum in its column. 
+
+![0719ZtW5ztQktBOJ](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0719ZtW5ztQktBOJ.png)
+
+### 题解
+本题遍历两遍, 将每行最小的值的下标和每列最大的值的下标分别放入两个数组, 数组的下标代表对应的行数和列数, 遍历最小值数组, 根据对应的下标在最大值数组中找到对应的值看是否与最小值数组中的下标相同. 相同则表名找到了一个lucky number. 通过提前构建最大值数组, 可以仅遍历一遍数组即同时找到每行的最小值和每列的最大值, 只需在遍历行的时候将每个数与当前该列的最大值比较并更新即可通过一遍遍历完成任务.
+
+### 代码
+```go 
+func luckyNumbers (matrix [][]int) []int {
+    rowlen := len(matrix)
+    colen := len(matrix[0])
+    minrow := make([]int, rowlen)
+    maxcol := make([]int, colen)
+    maxcolval := make([]int, colen)
+    for i, row := range matrix{
+        tempmin := 1000000
+        for j, num := range row{
+            if num < tempmin{
+                tempmin = num
+                minrow[i] = j
+            }
+            if num > maxcolval[j]{
+                maxcolval[j] = num
+                maxcol[j] = i
+            }
+        }
+    }
+    result := []int{}
+    for i, val := range minrow{
+        if maxcol[val] == i{
+            result = append(result, matrix[i][val])
+        }
+    }
+    return result
+}
+```