leetcode update

content/posts/leetcode.md

@@ -5925,3 +5925,67 @@ func deleteaNode(father *TreeNode, target int)bool{
 ### 总结
 
 直接返回节点会更简洁一些, 对于值符合的叶子节点, 递归时返回nil即可.
+
+## day81 2024-05-18
+
+### 979. Distribute Coins in Binary Tree
+
+You are given the root of a binary tree with n nodes where each node in the tree has node.val coins. There are n coins in total throughout the whole tree.
+
+In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent.
+
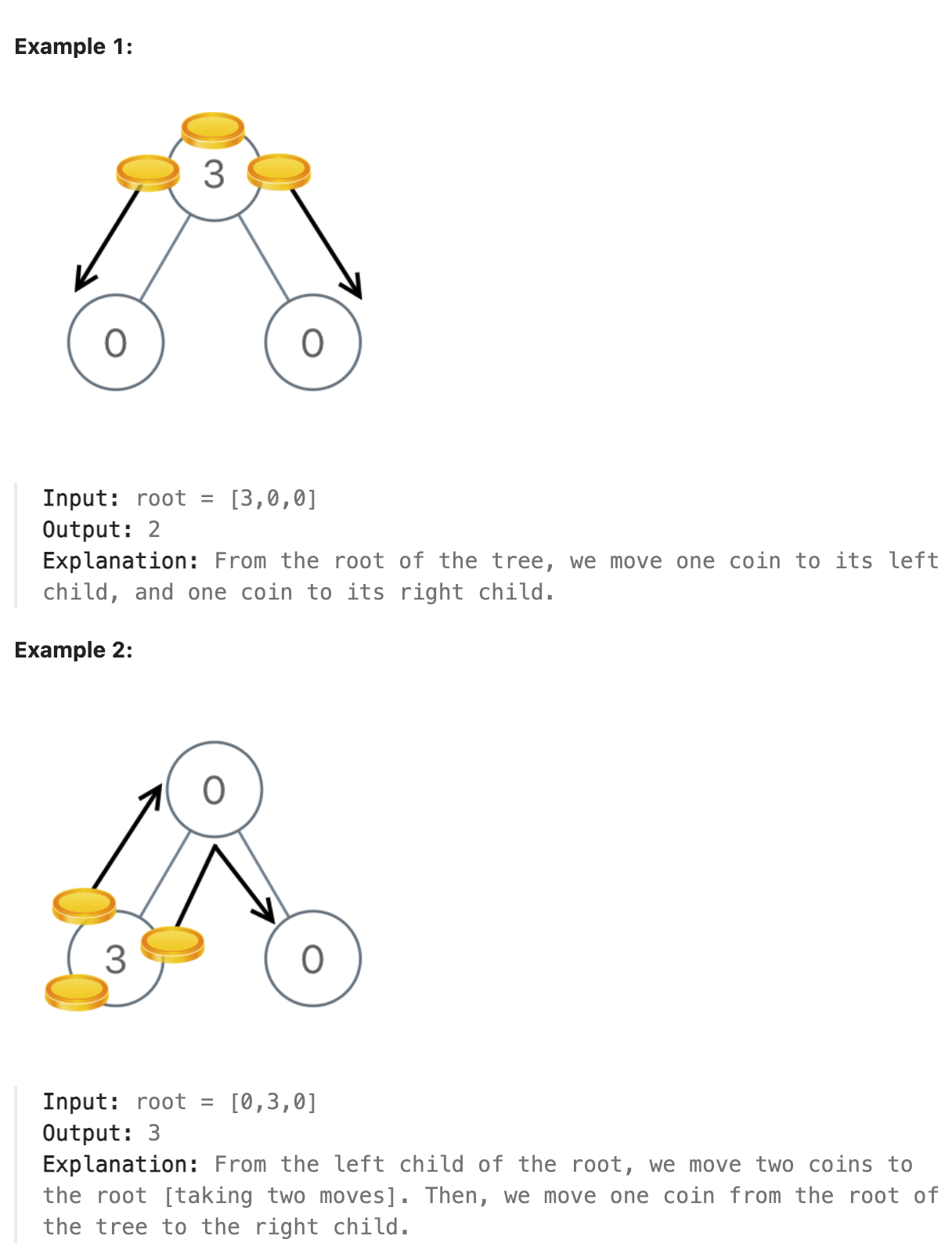
+Return the minimum number of moves required to make every node have exactly one coin.
+![0518KDVZu9LH37Ax](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0518KDVZu9LH37Ax.png)
+
+### 题解
+
+考虑仅有一个根节点和两个叶子节点的情况. 因为最终要得到每个节点仅有一个硬币, 因此叶子节点多余的硬币一定会被传递上去, 没有硬币的节点一定能从父节点获得一个硬币. 将硬币传递上去和从父节点获得硬币都需要与硬币数相等的步数. 因此对于每个父节点, 分别递归计算两个子树能给父节点的硬币数, 需要硬币用负数表示, 同时计算两个子树将每个节点都变为1个硬币到父节点时总共需要的步数. 对于叶子节点来说, 这样的操作即为, 若需要硬币则硬币数设为-1, 同时步数为1. 对于有多余硬币的叶子节点, 将多余的硬币设为硬币数, 同时步数设为多余的硬币数量. 进行后序遍历计算最终需要的步数即可.
+
+### 代码
+
+```go
+/**
+ * Definition for a binary tree node.
+ * type TreeNode struct {
+ *     Val int
+ *     Left *TreeNode
+ *     Right *TreeNode
+ * }
+ */
+func distributeCoins(root *TreeNode) int {
+    _, steps := caculatecoin(root)
+    return steps
+}
+
+func caculatecoin(father *TreeNode)(int, int){
+    needcoinleft, stepsleft, needcoinright, stepsright := 0,0,0,0
+    if father.Left == nil && father.Right == nil{
+        if father.Val == 0{
+            return -1,1
+        }else if father.Val > 1{
+            return father.Val-1, father.Val-1
+        }
+    }
+    if father.Left != nil{
+        needcoinleft, stepsleft = caculatecoin(father.Left)
+    }
+    if father.Right != nil{
+        needcoinright, stepsright = caculatecoin(father.Right)
+    }
+    needcoin := needcoinleft + needcoinright + father.Val - 1
+    steps := stepsleft + stepsright + abs(needcoin)
+    return needcoin, steps
+
+}
+
+func abs(num int)int{
+    if num < 0{
+        return -num
+    }
+    return num
+}
+```
+
+### 总结
+
+本题的关键之一在于理解把多余的硬币传上去和从父节点拿硬币从从步数上来说是等价的. 另一重要的等价性就是父节点和一个子节点都有多余硬币, 另一个子节点需要硬币时, 无论是把父节点的硬币分配给子节点还是把另一个子节点多余的硬币分配给子节点, 最终对步数的贡献都是相同的. 因为若把父节点的硬币给子节点(1步), 另一个子节点的硬币要向上传递(2步), 总共要3步. 而将另一个子节点的硬币分给这个子节点(2步), 父节点硬币向上传递(1步)也需要3步. 所以对于每个子树来说, 重要的是其能传递或者需要多少硬币, 至于内部分配情况对于总步数没有影响.