leetcode update

content/posts/leetcode.md

@@ -18032,3 +18032,153 @@ public:
     }
 };
 ```
+
+## day257 2024-11-20
+
+### 2516. Take K of Each Character From Left and Right
+
+You are given a string s consisting of the characters 'a', 'b', and 'c' and a non-negative integer k. Each minute, you may take either the leftmost character of s, or the rightmost character of s.
+
+Return the minimum number of minutes needed for you to take at least k of each character, or return -1 if it is not possible to take k of each character.
+
+![1120GQzlFRPPMxa3](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1120GQzlFRPPMxa3.png)
+
+### 题解
+
+本题要求返回能取得k个a,b,c字符需要的最少拿取次数，并不能使用贪心，因为选择从左面或者右面拿取字符会影响后面能得到目标结果时拿取的总个数，如左右都是字符a，但左侧第二个字符是b，右侧第二个字符是a，如果只需要每个字符拿1个，拿左侧的a后就可以继续拿取左侧的b，但若拿取右侧的a则想拿取b就要再拿掉左侧的a后才能拿到b。
+
+因此需要考虑左侧的选择会对右侧的选择造成什么影响，要把这种影响全部找出来并记录下来。因此可以找到刚好可以满足题目条件的左侧数组的长度，并将左侧指针指向这个子数组的末尾，在此情况下，当左侧指针向左移动时，左侧数组会不满足题目条件，因此需要右侧数组来补充缺少的字符使得总体满足题目条件，因此右侧指针向左移动直到移动过的部分的右侧数组包含的字符和左侧数组包含的字符和满足题目条件。计算此时左右子数组的长度和，如此反复，直到左侧指针移动到数组开头。
+
+但有可能数组本身就不可能满足题目要求，因此要先判断一下数组中存在的各个字符的个数，如果不满足要求直接返回-1。
+
+### 代码
+
+```cpp
+
+class Solution {
+public:
+    int takeCharacters(string s, int k) {
+      int ca=0,cb=0,cc=0;
+        int n=s.size();
+        int ans=n;
+        for(int i=0;i<n;i++){
+            if(s[i]=='a') ca++;
+            if(s[i]=='b') cb++;
+            if(s[i]=='c') cc++;
+        }
+        if(ca<k||cb<k||cc<k) return -1;
+        int i=n-1,j=n-1;
+        while(i>=0){
+            if(s[i]=='a') ca--;
+            if(s[i]=='b') cb--;
+            if(s[i]=='c') cc--;
+            while(ca<k||cb<k||cc<k){
+            if(s[j]=='a') ca++;
+            if(s[j]=='b') cb++;
+            if(s[j]=='c') cc++;
+                j--;
+            }
+            ans=min(ans,i+n-1-j); i--;
+        }
+        return ans;
+
+    }
+};
+```
+
+## day258 2024-11-21
+
+### 2257. Count Unguarded Cells in the Grid
+
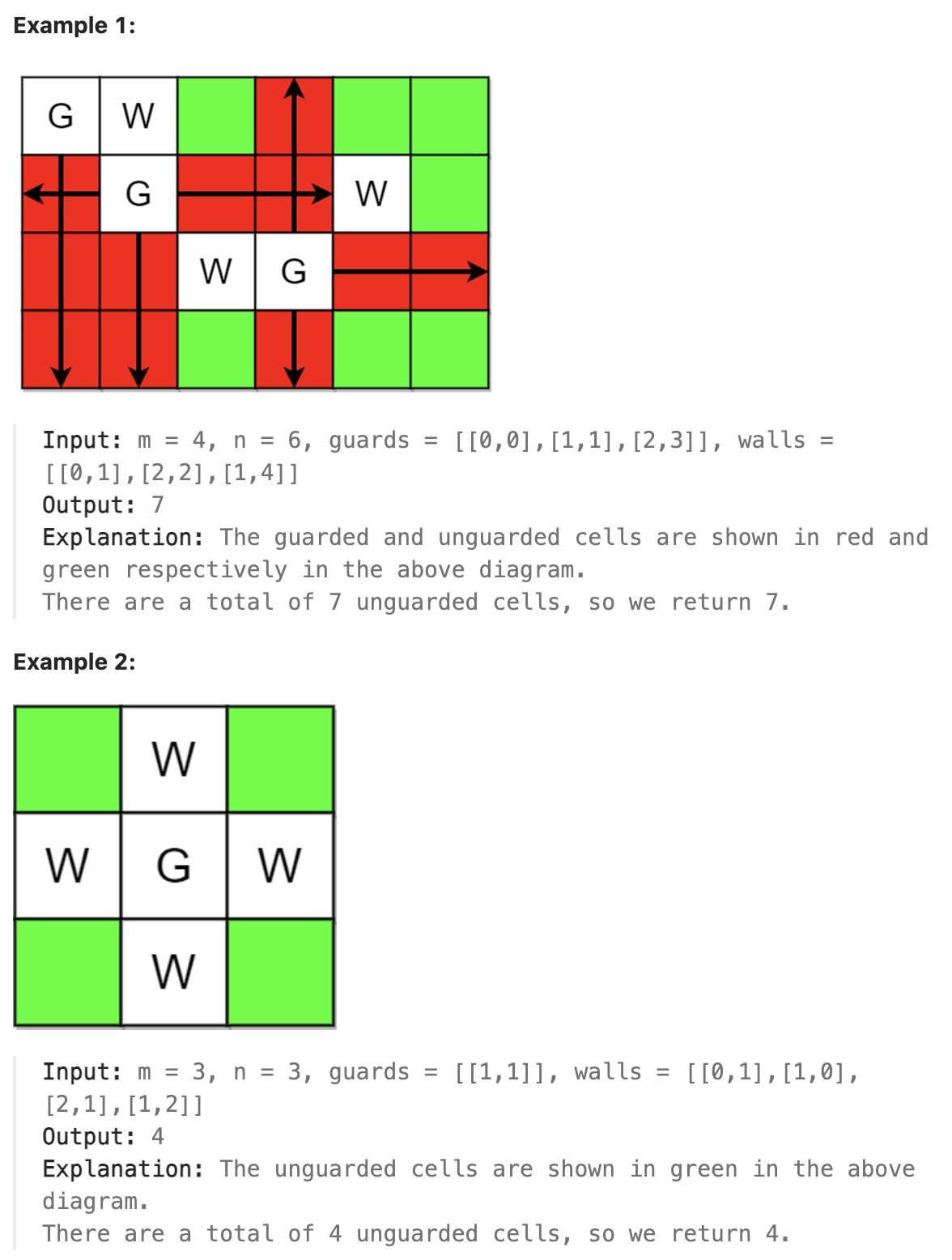
+You are given two integers m and n representing a 0-indexed m x n grid. You are also given two 2D integer arrays guards and walls where guards[i] = [rowi, coli] and walls[j] = [rowj, colj] represent the positions of the ith guard and jth wall respectively.
+
+A guard can see every cell in the four cardinal directions (north, east, south, or west) starting from their position unless obstructed by a wall or another guard. A cell is guarded if there is at least one guard that can see it.
+
+Return the number of unoccupied cells that are not guarded.
+
+![1121QXH56gcN6DEq](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1121QXH56gcN6DEq.png)
+
+### 题解
+
+本题模拟守卫能看到的区域，首先创建mxn的数组，先遍历所有墙的位置将对应位置的值设置为2，记录墙的个数，再遍历守卫，对每个守卫所在的位置向四个方向遍历直到到数组边界或者遇到墙为止，将这些位置的值设置为1，同时记录遍历过程中将0变为1的个数，最终用数组总数减去墙和守卫以及守卫看守的位置数的和得最终结果。
+
+这种遍历并且按照属性设置对应位置的值的方法可以得到正确的结果，但对有些示例会超时，思考为什么会超时以及如何优化，可以想到如果从某个守卫出发开始向某一方向（比如向右）遍历数组时遇到了另一个守卫，起始没有必要再继续向该方向遍历了，因为后面的位置遇到的新守卫同样也可以看到，此时可以直接结束遍历，因此我们可以将墙的位置值设置为3，将守卫位置的值先全部设置为2，在遍历数组时判断要遍历的位置的值是否小于2，这样就避免了多个守卫看同一个方向时对重叠看守的部分进行多次重复遍历。当然这里不会完全不重复，只是大大减少了重复量。
+
+### 代码
+
+```cpp
+class Solution {
+public:
+    int countUnguarded(int m, int n, vector<vector<int>>& guards, vector<vector<int>>& walls) {
+        vector<vector<int>> cells(m,vector<int>(n,0));
+        for (auto wall : walls){
+            cells[wall[0]][wall[1]] = 3;
+        }
+        int guardpos = 0;
+        int direction[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};
+        for (auto guard : guards){
+            cells[guard[0]][guard[1]] = 2;
+        }
+        for (auto guard : guards){
+            for(int i=0;i<4;i++){
+                int pos[2] = {guard[0]+direction[i][0], guard[1]+direction[i][1]};
+                while(pos[0]>=0&&pos[0]<m&&pos[1]>=0&&pos[1]<n&&cells[pos[0]][pos[1]]<2){
+                    if(cells[pos[0]][pos[1]] == 0){
+                        guardpos++;
+                        cells[pos[0]][pos[1]] = 1;
+                    }
+                    pos[0] += direction[i][0];
+                    pos[1] += direction[i][1];
+                }
+            }
+        }
+        return m*n-guardpos-guards.size()-walls.size();
+    }
+};
+```
+## day259 2024-11-22
+### 1072. Flip Columns For Maximum Number of Equal Rows 
+You are given an m x n binary matrix matrix.
+
+You can choose any number of columns in the matrix and flip every cell in that column (i.e., Change the value of the cell from 0 to 1 or vice versa).
+
+Return the maximum number of rows that have all values equal after some number of flips.
+
+![1122r0stlh0LaeX9](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1122r0stlh0LaeX9.png)
+
+### 题解
+本题先思考简单例子，对于两行01串，在什么情况下通过多次翻转同一个位置上的数字最终可以使得两行行内数字完全相同，如00，10显然无论怎么翻转都只可能有一行数字是完全相同的，另一行则不可能相同，再考虑10，01，只需翻转任意一列，两行数字都会相同。由此可以猜测对于任意两行数字，若这两行数字每一位上的数都不相同，则这两行数字最终可以通过翻转实现两行数字行内完全相同，注意数字只能取0，1两种，因此若两行数字满足每一位都不相同，要想三行数字满足行内相同，第三行数字必定和这两行数字中的某一行完全相同。
+
+则若能通过翻转使得任意两行的行内数字完全相同，这两行要么相同，要么相反。我们只需统计相同行和对应的相反行的数量和，找到最大值就得到本题的解。
+
+问题在于如何统计，考虑要统计的行要么完全相同，要么相反，则可以将二者用一个同样的值来表示，此处就要用到哈希，问题是如果将每一行中的每一位视为简单的二进制位，考虑行的长度最大为300，显然不能用整数直接装下，因此要么使用分块哈希，要么充分利用c++中已有的哈希实现，将每一行转换为字符串再作为哈希的键。由于相反的行我们想使用同一个键值来表示，因此对每一行都构造出该行对应的字符串和该行对应的相反行的字符串，取两个字符串中字典序小的字符串，这样就将相反行都用二者中字典序小的字符串来表示，进而统计满足相同或者相反行的总数。
+
+### 代码
+```cpp 
+class Solution {
+public:
+    int maxEqualRowsAfterFlips(vector<vector<int>>& matrix) {
+        unordered_map<string, int> count;
+        int m = matrix.size(), n = matrix[0].size();
+        
+        for (const auto& row : matrix) {
+            string pattern(n, '0');
+            string flipped(n, '0');
+            
+            for (int j = 0; j < n; j++) {
+                pattern[j] = row[j] + '0';
+                flipped[j] = (1 - row[j]) + '0';
+            }
+            
+            count[min(pattern, flipped)]++;
+        }
+        
+        int maxCount = 0;
+        for (const auto& [_, cnt] : count) {
+            maxCount = max(maxCount, cnt);
+        }
+        return maxCount;
+    }
+};
+
+```