mirror of
https://gitlab.com/game-loader/hugo.git
synced 2025-10-25 11:18:48 +08:00
leetcode update
This commit is contained in:
@ -21507,3 +21507,870 @@ public:
|
|||||||
}
|
}
|
||||||
};
|
};
|
||||||
```
|
```
|
||||||
|
## day312 2025-01-15
|
||||||
|
### 2429. Minimize XOR
|
||||||
|
Given two positive integers num1 and num2, find the positive integer x such that:
|
||||||
|
|
||||||
|
x has the same number of set bits as num2, and
|
||||||
|
The value x XOR num1 is minimal.
|
||||||
|
Note that XOR is the bitwise XOR operation.
|
||||||
|
|
||||||
|
Return the integer x. The test cases are generated such that x is uniquely determined.
|
||||||
|
|
||||||
|
The number of set bits of an integer is the number of 1's in its binary representation.
|
||||||
|
|
||||||
|

|
||||||
|
### 题解
|
||||||
|
本题可以分为两个任务,第一个计数num2中的二进制1的个数,第二个尝试与num1异或并得到一个最小的结果。对于第一个任务在昨天的问题中也有涉及,可以使用Brian Kernighan算法。要考虑的主要是第二个问题,当num2中二进制1的个数小于等于num1时,要想得到最小值,则与num1中的二进制1从左到右(从高位到低位)挨个异或,通过不断消除当前最高位的1来减少最多的值,最终得到一个最小的结果。
|
||||||
|
|
||||||
|
当num2中二进制1的个数大于num1时,首先肯定可以将num1中的1全部通过异或消除,但还有多余的1,这些1必然要与num1中的0异或得到1,此时的思路就与消除1时正好相反,要尽可能与num1中最低位的0异或这样才能增加最少的值最终得到最小的结果。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int minimizeXor(int num1, int num2) {
|
||||||
|
// 计算num2中1的个数
|
||||||
|
int count2 = 0;
|
||||||
|
int temp = num2;
|
||||||
|
while (temp) {
|
||||||
|
temp &= (temp - 1);
|
||||||
|
count2++;
|
||||||
|
}
|
||||||
|
|
||||||
|
int x = 0;
|
||||||
|
// 从最高位开始处理
|
||||||
|
for (int i = 31; i >= 0 && count2 > 0; i--) {
|
||||||
|
if (num1 & (1 << i)) {
|
||||||
|
x |= (1 << i);
|
||||||
|
count2--;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
// 如果还有剩余的1需要设置,从最低位开始找0位
|
||||||
|
for (int i = 0; count2 > 0 && i < 32; i++) {
|
||||||
|
if ((x & (1 << i)) == 0) { // 如果当前位是0
|
||||||
|
x |= (1 << i);
|
||||||
|
count2--;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
return x;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
## day313 2025-01-16
|
||||||
|
### 2425. Bitwise XOR of All Pairings
|
||||||
|
You are given two 0-indexed arrays, nums1 and nums2, consisting of non-negative integers. There exists another array, nums3, which contains the bitwise XOR of all pairings of integers between nums1 and nums2 (every integer in nums1 is paired with every integer in nums2 exactly once).
|
||||||
|
|
||||||
|
Return the bitwise XOR of all integers in nums3.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题要注意思考题目的实质,不能直接按照题目要求暴力计算。思考将nums1和nums2中的每个数字做异或后再将得到的结果做异或实际上和将nums1和nums2中的数字自身和自身做了多次异或后在将结果彼此之间异或的结果一样。即假设nums1中有a,b,nums2中有c,d则按照题目要求应该(a^c)^(a^d)^(b^c)^(b^d),这与(a^a)^(c^c)^(b^b)^(d^d)得到的结果相同,此处成立的原因是异或运算满足交换律。则可以发现将nums1中每个数字自身异或nums2数组长度的次数,将nums2中每个数字自身异或nums1长度的次数,最后将结果再异或就得到本题的结果。
|
||||||
|
|
||||||
|
则此时可以利用数字与自身异或的特性,一个数字和自身异或得到的值为0,再与自己异或得到数字自身,则与自身异或的次数为偶数次时为0,为奇数次时为数字自身。则先判断nums1和nums2的长度,若长度为偶数则另一个数组的不需要计算,必然全部为0,为奇数时另一个数组的数字全部进行异或即可得到结果。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int xorAllNums(vector<int>& nums1, vector<int>& nums2) {
|
||||||
|
int len1 = nums1.size();
|
||||||
|
int len2 = nums2.size();
|
||||||
|
int result = 0;
|
||||||
|
if(len1 % 2 == 1){
|
||||||
|
for(const int& num : nums2){
|
||||||
|
result ^= num;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
if(len2 % 2 == 1){
|
||||||
|
for(const int& num : nums1){
|
||||||
|
result ^= num;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
## day314 2025-01-17
|
||||||
|
### 2683. Neighboring Bitwise XOR
|
||||||
|
A 0-indexed array derived with length n is derived by computing the bitwise XOR (⊕) of adjacent values in a binary array original of length n.
|
||||||
|
|
||||||
|
Specifically, for each index i in the range [0, n - 1]:
|
||||||
|
|
||||||
|
If i = n - 1, then derived[i] = original[i] ⊕ original[0].
|
||||||
|
Otherwise, derived[i] = original[i] ⊕ original[i + 1].
|
||||||
|
Given an array derived, your task is to determine whether there exists a valid binary array original that could have formed derived.
|
||||||
|
|
||||||
|
Return true if such an array exists or false otherwise.
|
||||||
|
|
||||||
|
A binary array is an array containing only 0's and 1.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题仍然要思考问题的性质,异或后得到1说明两个数字不同,得到0说明两个数字相同。考虑a,b,c,如果a^b=c则a=c^b且b=c^a。也就是说,可以根据结果和其中一个数字恢复出另一个数字,则本题可以假设起始数字为0,则将起始数字直接与derived中的数字异或即可得到下一个数字,对下一个数字进行同样的操作直到derived中最后一个数字,最终得到的数字如果为0即和初始设定的数字相同则返回true,否则返回false。
|
||||||
|
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
bool doesValidArrayExist(vector<int>& derived) {
|
||||||
|
int num1 = 0;
|
||||||
|
for(const int& num : derived){
|
||||||
|
num1 ^= num;
|
||||||
|
}
|
||||||
|
if (num1 == 1){
|
||||||
|
return false;
|
||||||
|
}else{
|
||||||
|
return true;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
## day315 2025-01-18
|
||||||
|
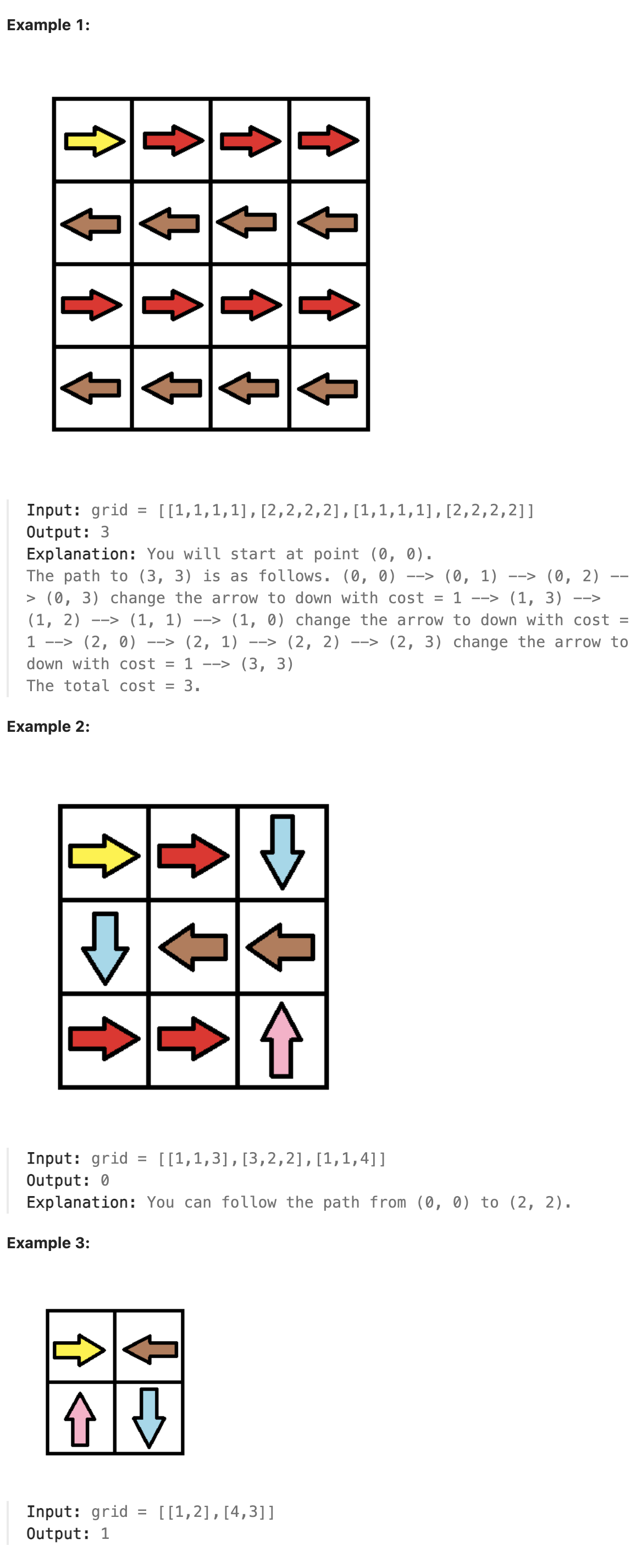
### 1368. Minimum Cost to Make at Least One Valid Path in a Grid
|
||||||
|
Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid\[i]\[j] can be:
|
||||||
|
|
||||||
|
1 which means go to the cell to the right. (i.e go from grid\[i]\[j] to grid\[i]\[j + 1])
|
||||||
|
2 which means go to the cell to the left. (i.e go from grid\[i]\[j] to grid\[i]\[j - 1])
|
||||||
|
3 which means go to the lower cell. (i.e go from grid\[i]\[j] to grid\[i + 1]\[j])
|
||||||
|
4 which means go to the upper cell. (i.e go from grid\[i]\[j] to grid\[i - 1]\[j])
|
||||||
|
Notice that there could be some signs on the cells of the grid that point outside the grid.
|
||||||
|
|
||||||
|
You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.
|
||||||
|
|
||||||
|
You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.
|
||||||
|
|
||||||
|
Return the minimum cost to make the grid have at least one valid path.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题是一道难题,问题的关键在于如何转化,本题给出的条件为原本指向的方向如果直接遍历则没有花费,想改变指向的方向就要花费1成本。这种向不同方向移动寻找路径的问题之前也做过类似的题目,尽管题中给出的是数组,但我们可以将其转化为一个图问题。因为题目中的数组本质上也只是图的一种表示,表示每个位置拥有的不同性质。
|
||||||
|
|
||||||
|
问题在于将其转化为一个什么样的图问题,图的要素就是点和边,那么如何将题目中的数组转化成不同的点和边呢,考虑到如果沿着每个位置指向的方向遍历则没有成本,因此可以给每个位置和其指向的方向的位置各构造一个点,从原本的点指向对应的指向方向的点的有向边权重为0表示没有成本,而指向其他方向的位置的有向边权重则为1表示要从当前的点走到这些位置需要1点花费,这样就成功的构造出了带边权的有向图,我们此时要找的就是一条权重和最小的从起始点到右下角点的路径,这就是一个最短路径问题,使用利用优先级队列实现的dijistra算法就可以解决。
|
||||||
|
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int minCost(vector<vector<int>>& grid) {
|
||||||
|
int m = grid.size(), n = grid[0].size();
|
||||||
|
priority_queue<vector<int>, vector<vector<int>>, greater<>> pq;
|
||||||
|
vector<vector<int>> dist(m, vector<int>(n, INT_MAX));
|
||||||
|
|
||||||
|
vector<pair<int, int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
|
||||||
|
|
||||||
|
pq.push({0, 0, 0});
|
||||||
|
dist[0][0] = 0;
|
||||||
|
|
||||||
|
while (!pq.empty()) {
|
||||||
|
auto curr = pq.top();
|
||||||
|
pq.pop();
|
||||||
|
|
||||||
|
int cost = curr[0];
|
||||||
|
int row = curr[1];
|
||||||
|
int col = curr[2];
|
||||||
|
|
||||||
|
if (cost > dist[row][col]) continue;
|
||||||
|
|
||||||
|
for (int i = 0; i < 4; i++) {
|
||||||
|
int newRow = row + dirs[i].first;
|
||||||
|
int newCol = col + dirs[i].second;
|
||||||
|
|
||||||
|
if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n) {
|
||||||
|
int newCost = cost + (grid[row][col] == i + 1 ? 0 : 1);
|
||||||
|
|
||||||
|
// 如果找到更好的路径,更新并加入队列
|
||||||
|
if (newCost < dist[newRow][newCol]) {
|
||||||
|
dist[newRow][newCol] = newCost;
|
||||||
|
pq.push({newCost, newRow, newCol});
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
return dist[m-1][n-1];
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
## day316 2025-01-19
|
||||||
|
### 407. Trapping Rain Water II
|
||||||
|
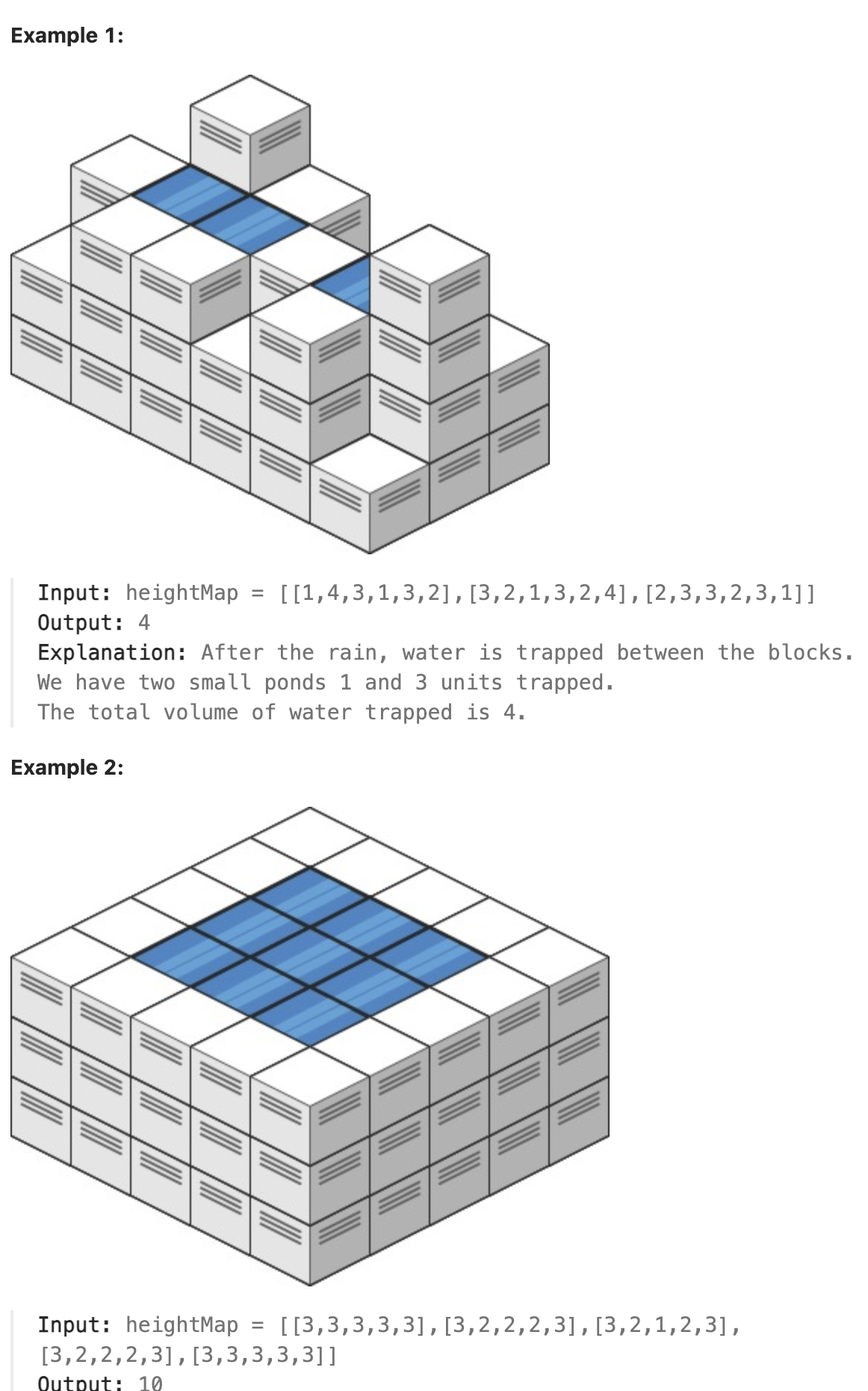
Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题是一道难题,刚看到本题可能会想到另一道经典的接雨水,即一维的接雨水,也可能会想到或许可以使用和另一道题类似的解法,接雨水经典的解法是动态规划,分别从首尾遍历数组得到各个位置左右的最大值,取两个最大值中较小的那个与当前位置高度相减即得当前位置能接的雨水,这种解法的好处在于,不需要知道最大值具体对应的位置,只需知道最大值是什么就可以解决问题。如果本题使用类似的解法则应对行列也采用同样的方式得到每个位置四个方向的最大值,取其中最小的那个。但这种方法有很大的问题,因为这是一个二维平面,如果一个位置相邻位置对应的四个方向中的值有小于当前位置对应的四个方向值中最小的那个,则这个位置的雨水会顺着相邻位置再从更小的边界流出去,所以当前位置四个方向中最大值的最小值并没有太多用处。
|
||||||
|
|
||||||
|
此时要思考,采用类似的方式解题为什么不能得到正确答案。在一维的情况下,边界的限制就是左右两侧的墙壁,但在二维的情况下,边界并不仅仅是该位置对应的四个方向构成的十字范围内的墙壁,而是整个平面内的墙壁。即四周一圈,考虑三行四列的情况,四周一圈肯定不能接雨水,只有中间两个空位可以用于接雨水,对于这两个位置来说,假设两个位置原始高度都为0,则两个位置能接的雨水高度取决于四周一圈(除了四个角以外)的围墙中高度的最小值。假如(1,2)位置处的高度高于(1,3)位置,则(1,1)位置对应的围墙其实就变成了紧挨着它的四周一圈,此刻我们发现解决该问题的关键在于找到每个位置对应的四周一圈围墙的最小值。
|
||||||
|
|
||||||
|
如果选定随意一个位置,来想办法确定该位置对应的四周一圈的围墙都是在什么位置并且其中最小值是什么是比较困难的,因此我们要想办法通过某种方式来递进式的不断缩小围墙,从而确定某个区域对应的围墙是哪里。考虑之前提到的三行四列的情况,初始可以假定四周一圈作为围墙,因为位于四周一圈的任何位置都不可能存雨水,随后向内收缩来慢慢得到每个位置对应的围墙。此时可以挑选四周一圈中除四个角外的最小值,由这个最小值出发向内遍历,假如此时(0,1)处的围墙为最小值,则查看(1,1)位置的高度(此时查看1,2位置没有用,因为在不知道1,1位置高度情况时不能确定1,2处的水会不会从0,1流走,若1,1高于0,1则可以确定不会从0,1流走,此时再去找会从哪里流走,低于则就会从0,1流走),有两种情况,若(1,1)位置处高度小于(0,1),则(0,1)仍可以作为围墙,而(1,1)处可以接的雨水即为(1,1)的高度和(0,1)高度的差,若(1,1)位置处高度大于(0,1),则(1,1)作为新的围墙,将(0,1)从围墙中踢出,则发现可以保存一个围墙的最小堆,保存全部围墙的位置和对应的高度,从堆顶弹出当前围墙的最小值,使用bfs遍历最小值的相邻位置,对于小于最小值的位置计算可以接的雨水高度加入总和,并将该位置放入最小堆,高度设定为最小值的高度。对大于最小值的位置,将该位置自身的高度和位置放入最小堆。其实这一操作和一维情况下的接雨水的预处理过程类似,一维情况下,从前向后遍历时,如果当前位置高度小于左侧的最大高度,则后面还是要和之前的最大高度比较,相当于这个位置继承了左侧的最大高度,而大于左侧最大高度时则更新最大高度,相当于重新设置最大高度。本题中对于小于围墙最小值的位置,继承围墙最小值的高度并继续遍历访问该位置相邻的位置,大于则重新设定围墙。若深刻理解了经典的一维接雨水问题的解法,在本题能想到将原来的一维的两侧高度转化为一圈的围墙高度,并想到可以在初始假定四周一圈为起始围墙则后续的思路与一维的问题十分相似,只是处理一维时是直接向后遍历,二维时是寻找相邻,但本质上都是一种处理相邻元素并更新状态的思路。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int trapRainWater(vector<vector<int>>& heightMap) {
|
||||||
|
if (heightMap.empty() || heightMap[0].empty()) return 0;
|
||||||
|
|
||||||
|
int m = heightMap.size();
|
||||||
|
int n = heightMap[0].size();
|
||||||
|
if (m <= 2 || n <= 2) return 0;
|
||||||
|
|
||||||
|
priority_queue<pair<int, pair<int, int>>,
|
||||||
|
vector<pair<int, pair<int, int>>>,
|
||||||
|
greater<pair<int, pair<int, int>>>> pq;
|
||||||
|
|
||||||
|
// 访问标记数组
|
||||||
|
vector<vector<bool>> visited(m, vector<bool>(n, false));
|
||||||
|
|
||||||
|
for (int j = 0; j < n; j++) {
|
||||||
|
pq.push({heightMap[0][j], {0, j}});
|
||||||
|
pq.push({heightMap[m-1][j], {m-1, j}});
|
||||||
|
visited[0][j] = true;
|
||||||
|
visited[m-1][j] = true;
|
||||||
|
}
|
||||||
|
for (int i = 1; i < m-1; i++) {
|
||||||
|
pq.push({heightMap[i][0], {i, 0}});
|
||||||
|
pq.push({heightMap[i][n-1], {i, n-1}});
|
||||||
|
visited[i][0] = true;
|
||||||
|
visited[i][n-1] = true;
|
||||||
|
}
|
||||||
|
|
||||||
|
const int dx[4] = {-1, 1, 0, 0};
|
||||||
|
const int dy[4] = {0, 0, -1, 1};
|
||||||
|
|
||||||
|
int result = 0;
|
||||||
|
while (!pq.empty()) {
|
||||||
|
auto curr = pq.top();
|
||||||
|
pq.pop();
|
||||||
|
int height = curr.first;
|
||||||
|
int row = curr.second.first;
|
||||||
|
int col = curr.second.second;
|
||||||
|
|
||||||
|
for (int i = 0; i < 4; i++) {
|
||||||
|
int newRow = row + dx[i];
|
||||||
|
int newCol = col + dy[i];
|
||||||
|
|
||||||
|
if (newRow >= 0 && newRow < m &&
|
||||||
|
newCol >= 0 && newCol < n &&
|
||||||
|
!visited[newRow][newCol]) {
|
||||||
|
|
||||||
|
visited[newRow][newCol] = true;
|
||||||
|
if (heightMap[newRow][newCol] < height) {
|
||||||
|
result += height - heightMap[newRow][newCol];
|
||||||
|
pq.push({height, {newRow, newCol}});
|
||||||
|
} else {
|
||||||
|
// 如果新位置高度大于等于当前围墙,将成为新的围墙
|
||||||
|
pq.push({heightMap[newRow][newCol], {newRow, newCol}});
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
## day317 2025-01-20
|
||||||
|
### 2661. First Completely Painted Row or Column
|
||||||
|
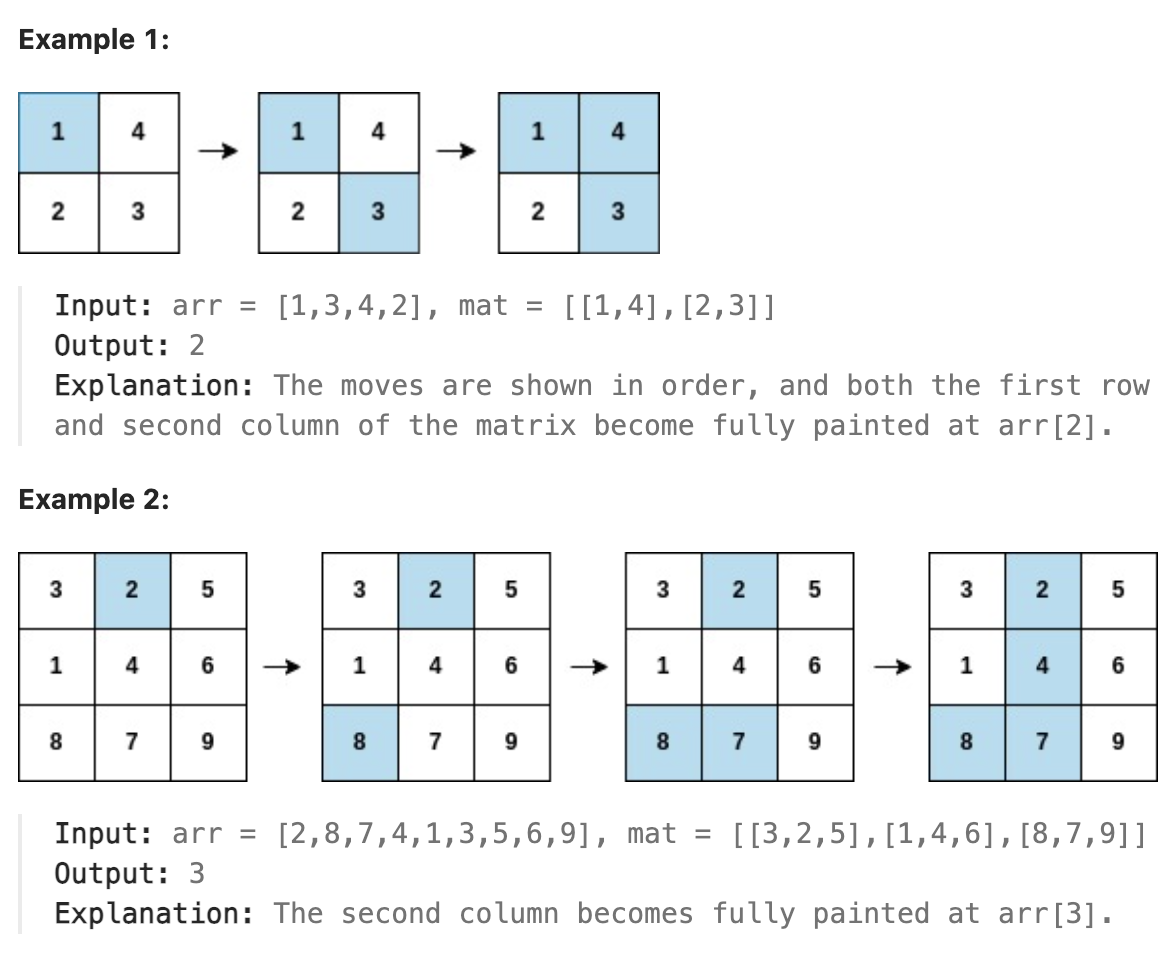
You are given a 0-indexed integer array arr, and an m x n integer matrix mat. arr and mat both contain all the integers in the range [1, m * n].
|
||||||
|
|
||||||
|
Go through each index i in arr starting from index 0 and paint the cell in mat containing the integer arr[i].
|
||||||
|
|
||||||
|
Return the smallest index i at which either a row or a column will be completely painted in mat.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题先遍历mat,将每个数字对应的位置记录下来(注意数字均不重复,故可以使用数组来保存),再构建两个数组分别用于记录行和列中已经被涂的格子的个数,再遍历arr,根据arr中数字的位置将对应行列的被涂格子数加一,判断当前行或者列是否已经涂满,涂满返回当前数字下标。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int firstCompleteIndex(vector<int>& arr, vector<vector<int>>& mat) {
|
||||||
|
int m = mat.size();
|
||||||
|
int n = mat[0].size();
|
||||||
|
|
||||||
|
vector<pair<int, int>> pos(m * n + 1);
|
||||||
|
for (int i = 0; i < m; i++) {
|
||||||
|
for (int j = 0; j < n; j++) {
|
||||||
|
pos[mat[i][j]] = {i, j};
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
vector<int> rowCount(m, 0);
|
||||||
|
vector<int> colCount(n, 0);
|
||||||
|
|
||||||
|
for (int i = 0; i < arr.size(); i++) {
|
||||||
|
auto [row, col] = pos[arr[i]];
|
||||||
|
rowCount[row]++;
|
||||||
|
colCount[col]++;
|
||||||
|
|
||||||
|
if (rowCount[row] == n || colCount[col] == m) {
|
||||||
|
return i;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
return -1;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
## day318 2025-01-21
|
||||||
|
### 2017. Grid Game
|
||||||
|
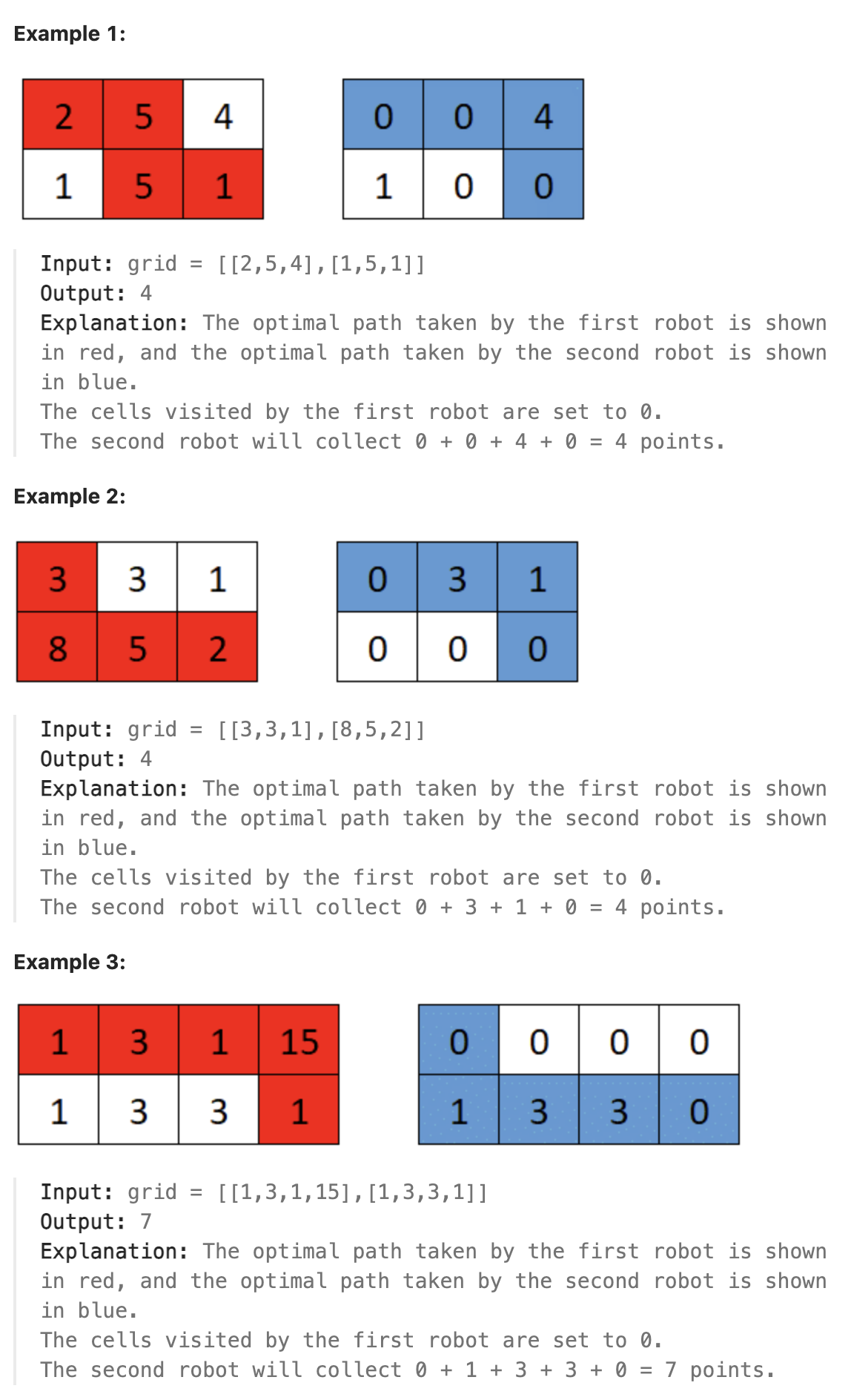
You are given a 0-indexed 2D array grid of size 2 x n, where grid\[r]\[c] represents the number of points at position (r, c) on the matrix. Two robots are playing a game on this matrix.
|
||||||
|
|
||||||
|
Both robots initially start at (0, 0) and want to reach (1, n-1). Each robot may only move to the right ((r, c) to (r, c + 1)) or down ((r, c) to (r + 1, c)).
|
||||||
|
|
||||||
|
At the start of the game, the first robot moves from (0, 0) to (1, n-1), collecting all the points from the cells on its path. For all cells (r, c) traversed on the path, grid\[r]\[c] is set to 0. Then, the second robot moves from (0, 0) to (1, n-1), collecting the points on its path. Note that their paths may intersect with one another.
|
||||||
|
|
||||||
|
The first robot wants to minimize the number of points collected by the second robot. In contrast, the second robot wants to maximize the number of points it collects. If both robots play optimally, return the number of points collected by the second robot.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题注意机器人只能向右或者向下移动,因此经过的路径具有很明确的方向性,还要注意一个非常重要的条件,即grid矩阵只有两行,只有两行意味着第一个机器人只能选择在某个位置向下移动后一直向右移动,也就意味着第一个机器人在第一行只会从开头移动到中间某个位置i,而在第二行则会从i开始一直向后移动到第二行末尾。只有两行这个条件的存在使得问题大大简化,因为第二个机器人在移动时要么选择获得第一行从i开始向后的全部位置的数字,要么选择从第二行开头开始到i-1的全部位置的数字。则要想使得第二个机器人能得到的总和尽可能小,就要使从i开始到末尾的和与第二行从开头到i的和都尽可能小。则可以计算出两行的前缀和和两行的总和,对每个i,都计算出第一行从i到末尾的和与第二行从开头到i-1的和并比较二者,取二者中较大的值(第二个机器人会选择更大的路径),并与记录的全局记录值比较,如果比全局记录更小则更新全局记录。最后返回全局记录。
|
||||||
|
|
||||||
|
如果本题是三行或者更多,则这种解法就不适用了,因此只有两行是一个很重要的条件。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
long long gridGame(vector<vector<int>>& grid) {
|
||||||
|
long long int row1 = 0;
|
||||||
|
long long int row2 = 0;
|
||||||
|
int cols = grid[0].size();
|
||||||
|
vector<long long int> prefix1(cols+1,0);
|
||||||
|
vector<long long int> prefix2(cols+1,0);
|
||||||
|
for(int i=0;i<cols;i++){
|
||||||
|
row1 += grid[0][i];
|
||||||
|
prefix1[i+1] = row1;
|
||||||
|
row2 += grid[1][i];
|
||||||
|
prefix2[i+1] = row2;
|
||||||
|
}
|
||||||
|
long long int current = 0;
|
||||||
|
long long int result = LLONG_MAX ;
|
||||||
|
for(int i=1;i<=cols;i++){
|
||||||
|
current = max(row1-prefix1[i],prefix2[i-1]);
|
||||||
|
result = min(result, current);
|
||||||
|
}
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
## day319 2025-01-22
|
||||||
|
### 1765. Map of Highest Peak
|
||||||
|
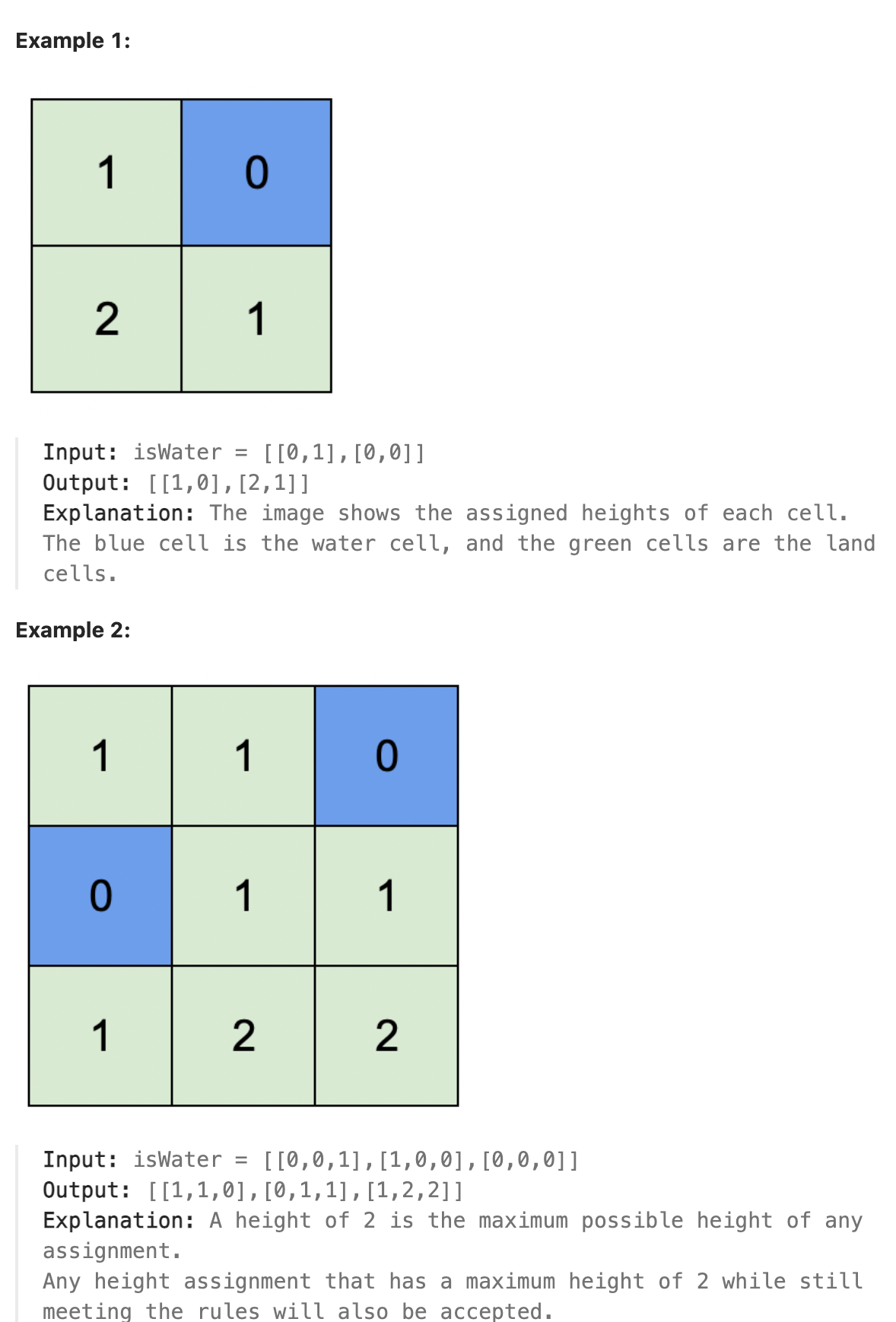
You are given an integer matrix isWater of size m x n that represents a map of land and water cells.
|
||||||
|
|
||||||
|
If isWater\[i]\[j] == 0, cell (i, j) is a land cell.
|
||||||
|
If isWater\[i]\[j] == 1, cell (i, j) is a water cell.
|
||||||
|
You must assign each cell a height in a way that follows these rules:
|
||||||
|
|
||||||
|
The height of each cell must be non-negative.
|
||||||
|
If the cell is a water cell, its height must be 0.
|
||||||
|
Any two adjacent cells must have an absolute height difference of at most 1. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
|
||||||
|
Find an assignment of heights such that the maximum height in the matrix is maximized.
|
||||||
|
|
||||||
|
Return an integer matrix height of size m x n where height\[i]\[j] is cell (i, j)'s height. If there are multiple solutions, return any of them.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题要读懂题面,注意要求相邻两个格子的差值最多为1,而水面的高度必须为0,则以水面为基准,水面的相邻格子高度必定为0或者1,为了最终能得到尽可能大的最大值,必然要选择让水面相邻格子的高度增加即均为1,对于得到的全部高度为1的的格子,同样对这些格子的相邻格子由于题面限制,这些格子的相邻格子的高度必定为2,以此迭代直到全部格子都被填满,最后被填充的格子的高度即为得到的最大高度。
|
||||||
|
|
||||||
|
则此过程可以使用bfs来解决,先将所有的水面位置放入队列,再依次执行bfs,将所有水面的相邻位置高度设为1并放入队列,继续对高度为1的格子执行bfs,以此类推。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
|
||||||
|
int m = isWater.size();
|
||||||
|
int n = isWater[0].size();
|
||||||
|
|
||||||
|
vector<vector<int>> height(m, vector<int>(n, -1));
|
||||||
|
queue<pair<int, int>> q;
|
||||||
|
|
||||||
|
for (int i = 0; i < m; i++) {
|
||||||
|
for (int j = 0; j < n; j++) {
|
||||||
|
if (isWater[i][j] == 1) {
|
||||||
|
height[i][j] = 0;
|
||||||
|
q.push({i, j});
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
vector<int> dx = {-1, 0, 1, 0};
|
||||||
|
vector<int> dy = {0, 1, 0, -1};
|
||||||
|
|
||||||
|
// BFS过程
|
||||||
|
while (!q.empty()) {
|
||||||
|
int x = q.front().first;
|
||||||
|
int y = q.front().second;
|
||||||
|
q.pop();
|
||||||
|
|
||||||
|
for (int i = 0; i < 4; i++) {
|
||||||
|
int nx = x + dx[i];
|
||||||
|
int ny = y + dy[i];
|
||||||
|
|
||||||
|
if (nx >= 0 && nx < m && ny >= 0 && ny < n && height[nx][ny] == -1) {
|
||||||
|
height[nx][ny] = height[x][y] + 1;
|
||||||
|
q.push({nx, ny});
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
return height;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
## day320 2025-01-23
|
||||||
|
### 1267. Count Servers that Communicate
|
||||||
|
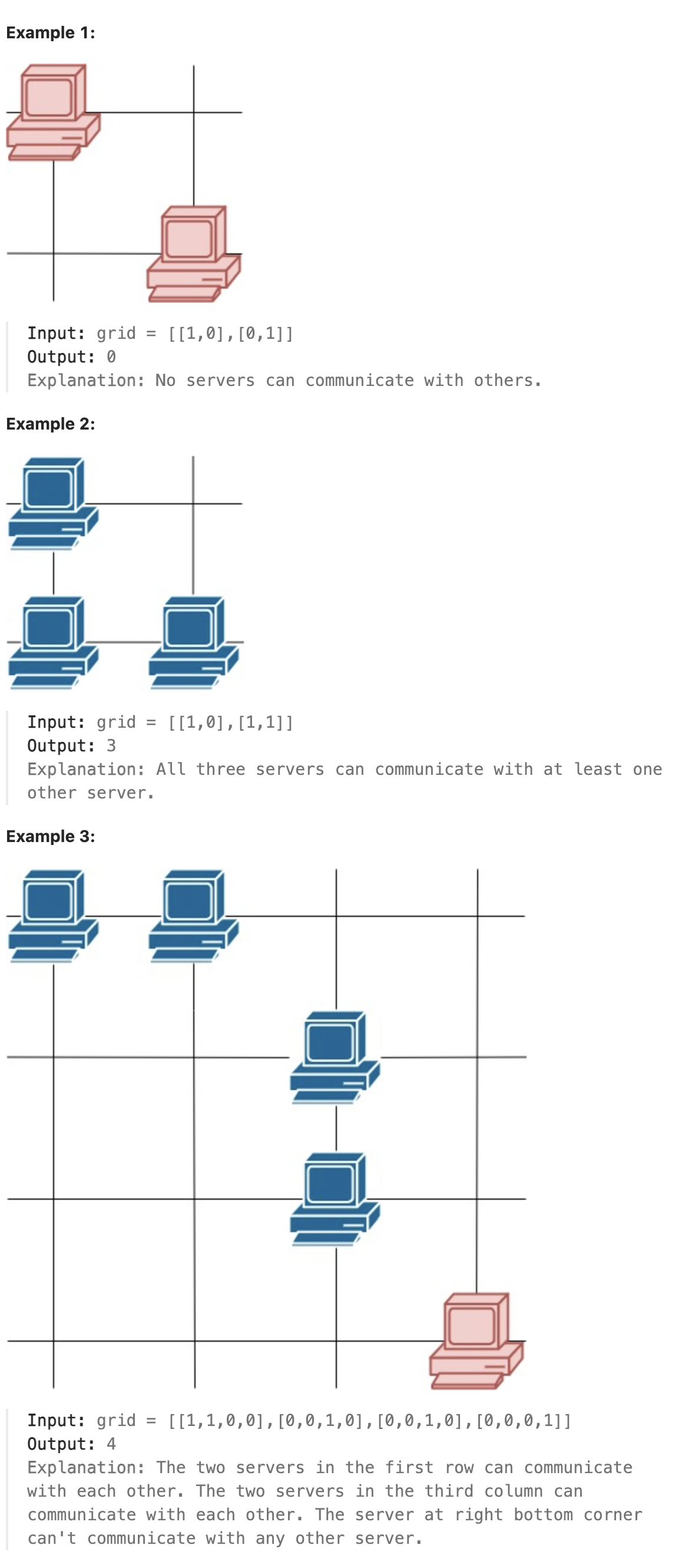
You are given a map of a server center, represented as a m * n integer matrix grid, where 1 means that on that cell there is a server and 0 means that it is no server. Two servers are said to communicate if they are on the same row or on the same column.
|
||||||
|
|
||||||
|
Return the number of servers that communicate with any other server.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题只要在同一行或者同一列的服务就可以相互通信,因此记录行或者列是否出现过服务,后续同一行或者同一列的其余服务就一定可以满足题目条件与其他服务通信。则可直接遍历整个数组,记录每一行每一列出现了多少个服务,再从头遍历数组,如果当前位置存在服务且行和列的服务存在个数大于1,说明当前位置可以与其他服务通信,即可加入计数当中。
|
||||||
|
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int countServers(vector<vector<int>>& grid) {
|
||||||
|
int m = grid.size();
|
||||||
|
int n = grid[0].size();
|
||||||
|
vector<int> rowCount(m, 0);
|
||||||
|
vector<int> colCount(n, 0);
|
||||||
|
|
||||||
|
// 第一次遍历:统计每行每列的服务器数量
|
||||||
|
for (int i = 0; i < m; i++) {
|
||||||
|
for (int j = 0; j < n; j++) {
|
||||||
|
if (grid[i][j] == 1) {
|
||||||
|
rowCount[i]++;
|
||||||
|
colCount[j]++;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
// 第二次遍历:统计可以通信的服务器
|
||||||
|
int result = 0;
|
||||||
|
for (int i = 0; i < m; i++) {
|
||||||
|
for (int j = 0; j < n; j++) {
|
||||||
|
if (grid[i][j] == 1) {
|
||||||
|
if (rowCount[i] > 1 || colCount[j] > 1) {
|
||||||
|
result++;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
## day321 2025-01-24
|
||||||
|
### 802. Find Eventual Safe States
|
||||||
|
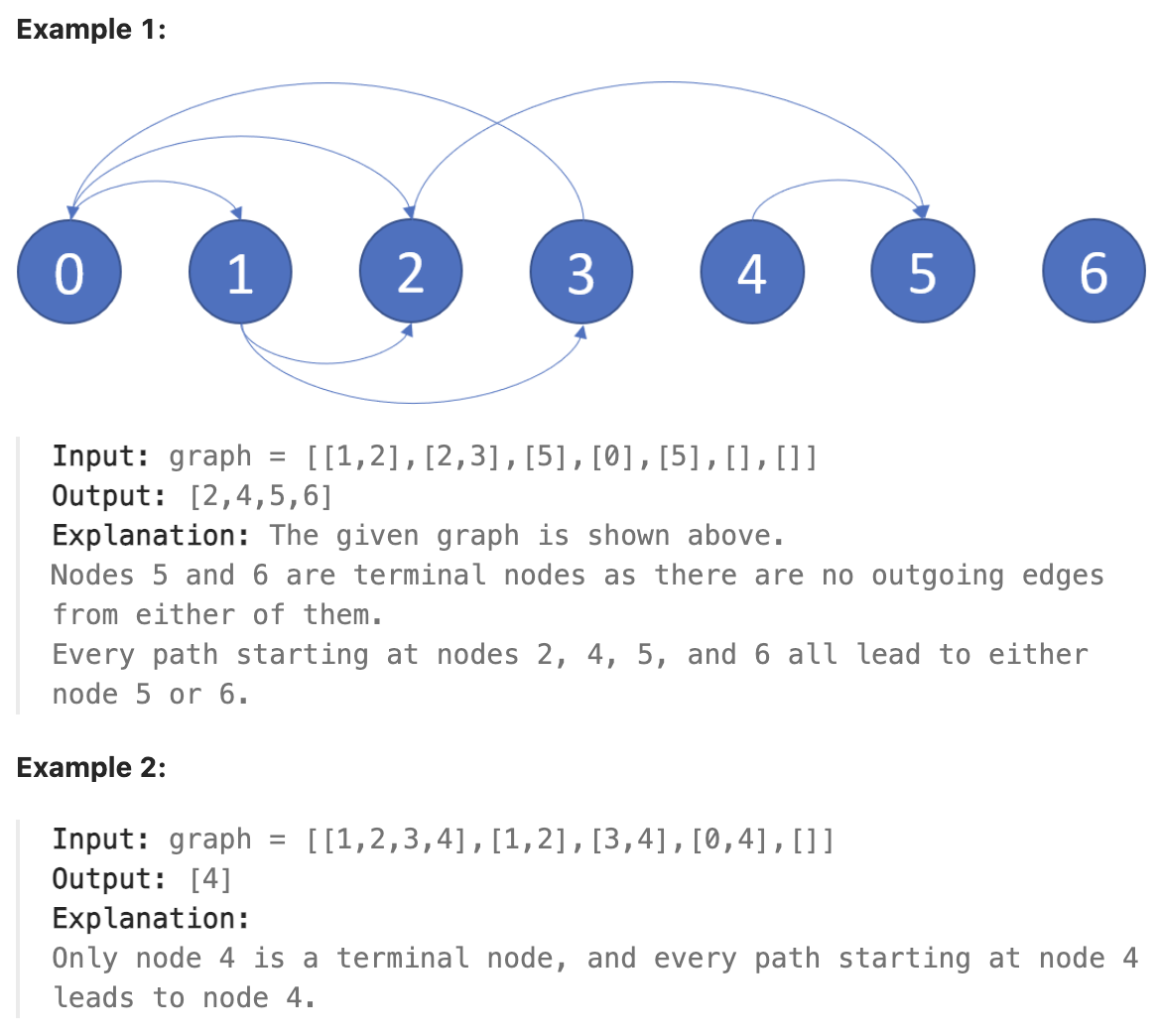
There is a directed graph of n nodes with each node labeled from 0 to n - 1. The graph is represented by a 0-indexed 2D integer array graph where graph[i] is an integer array of nodes adjacent to node i, meaning there is an edge from node i to each node in graph[i].
|
||||||
|
|
||||||
|
A node is a terminal node if there are no outgoing edges. A node is a safe node if every possible path starting from that node leads to a terminal node (or another safe node).
|
||||||
|
|
||||||
|
Return an array containing all the safe nodes of the graph. The answer should be sorted in ascending order.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题先考虑如何找到终结节点,根据题目如果一个节点上没有出边那么该节点就为终结节点,则遍历graph,所有没有出边的下标对应的节点均为终结节点。在遍历graph时,既可以得到所有节点对应的后继节点,也可以得到所有节点对应的全部前置节点,则对全部的终结节点,将其全部放入队列,遍历其全部的前置节点,这些节点均有指向终结节点的有向边,可能为安全节点,判断这些节点是否为安全节点,如果是则更新安全节点的状态数组,并将该节点放入队列中。不是则跳过继续向后遍历。如此反复即可得到全部安全节点。
|
||||||
|
|
||||||
|
这种方式可以得到结果的关键在于,以终结节点作为终点反向进行拓扑排序,先遍历到的指向终结节点的节点中只有仅包含指向终结节点一条边的节点会被认为是安全节点,再继续遍历得到的这些安全节点的前置节点,就可得到仅指向这些安全节点的或者同时指向安全节点和终结节点的新的安全节点,相当于每次都在得到新的安全节点的基础上在可能变为安全节点的节点中寻找哪些是新的安全节点。
|
||||||
|
|
||||||
|
本题也可以构造一个反向图,将原图中全部的边反向,则终结节点此时变为起始节点,遍历这些起始节点的后续节点,删掉起始节点和后续节点之间的边,找到所有入度变为0的节点即为安全节点,再在这些节点的基础上继续向后遍历反向图中的后续节点,执行同样的操作,每次都找到入度变为0的节点继续遍历,如此反复直到无法继续遍历即得全部安全节点。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
|
||||||
|
int n = graph.size();
|
||||||
|
vector<vector<int>> prevNodes(n);
|
||||||
|
vector<bool> canReachTerminal(n, false);
|
||||||
|
vector<int> terminalNodes;
|
||||||
|
|
||||||
|
// 找出终结节点并构建前置节点关系
|
||||||
|
for(int i = 0; i < n; i++) {
|
||||||
|
if(graph[i].empty()) {
|
||||||
|
terminalNodes.push_back(i);
|
||||||
|
canReachTerminal[i] = true;
|
||||||
|
}
|
||||||
|
// 构建前置节点关系
|
||||||
|
for(int next : graph[i]) {
|
||||||
|
prevNodes[next].push_back(i);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
queue<int> q;
|
||||||
|
for(int node : terminalNodes) {
|
||||||
|
q.push(node);
|
||||||
|
}
|
||||||
|
|
||||||
|
while(!q.empty()) {
|
||||||
|
int curr = q.front();
|
||||||
|
q.pop();
|
||||||
|
|
||||||
|
// 遍历当前节点的所有前置节点
|
||||||
|
for(int prev : prevNodes[curr]) {
|
||||||
|
if(!canReachTerminal[prev]) {
|
||||||
|
// 检查prev的所有后继节点是否都可以到达终结节点
|
||||||
|
bool allNextCanReach = true;
|
||||||
|
for(int next : graph[prev]) {
|
||||||
|
if(!canReachTerminal[next]) {
|
||||||
|
allNextCanReach = false;
|
||||||
|
break;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
if(allNextCanReach) {
|
||||||
|
canReachTerminal[prev] = true;
|
||||||
|
q.push(prev);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
vector<int> result;
|
||||||
|
for(int i = 0; i < n; i++) {
|
||||||
|
if(canReachTerminal[i]) {
|
||||||
|
result.push_back(i);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
## day322 2025-01-25
|
||||||
|
### 2948. Make Lexicographically Smallest Array by Swapping elements
|
||||||
|
You are given a 0-indexed array of positive integers nums and a positive integer limit.
|
||||||
|
|
||||||
|
In one operation, you can choose any two indices i and j and swap nums[i] and nums[j] if |nums[i] - nums[j]| <= limit.
|
||||||
|
|
||||||
|
Return the lexicographically smallest array that can be obtained by performing the operation any number of times.
|
||||||
|
|
||||||
|
An array a is lexicographically smaller than an array b if in the first position where a and b differ, array a has an element that is less than the corresponding element in b. For example, the array [2,10,3] is lexicographically smaller than the array [10,2,3] because they differ at index 0 and 2 < 10.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题考虑对任意数字m,能与其交换位置的数字的范围在m-limit\~m+limit之间。如果存在m+limit这一数字,则实际m可交换的数字范围就扩大为m-limit\~m+limit+limit之间。因为m总可以通过先让m+limit和更大的数字交换位置再让m和m+limit交换位置来与更大的数字交换位置,此时可互相交换位置的数字范围变为m-limit\~m+limit+limit。只要记录下该范围内的全部数字及其位置,再对范围内的全部数字排序,按序放在范围内对应的全部位置上。
|
||||||
|
|
||||||
|
对于在范围外的数字,则需要同样记录其可交换位置的范围,这样我们需要记录不同的范围,范围内已经存在的数字和这些数字对应的下标。每个范围内的数字相当于一个集合,集合内的的数字都有共同的性质即可以任意交换位置。则先对数字排序,依序将相邻的满足limit差值的数字放入同一个集合(可以用数组实现)。再对同一个集合内的数字对应的全部下标排序,将数字自身依序依次放入对应的下标中。最终即得到结果。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
vector<int> lexicographicallySmallestArray(vector<int>& nums, int limit) {
|
||||||
|
int n = nums.size();
|
||||||
|
vector<pair<int, int>> pairs;
|
||||||
|
for (int i = 0; i < n; i++) {
|
||||||
|
pairs.push_back({nums[i], i});
|
||||||
|
}
|
||||||
|
|
||||||
|
sort(pairs.begin(), pairs.end());
|
||||||
|
|
||||||
|
vector<int> result(n);
|
||||||
|
for (int i = 0, j = 0; i < n; i = j) {
|
||||||
|
j = i + 1;
|
||||||
|
while (j < n && pairs[j].first - pairs[j-1].first <= limit) {
|
||||||
|
j++;
|
||||||
|
}
|
||||||
|
|
||||||
|
vector<int> indices;
|
||||||
|
for (int k = i; k < j; k++) {
|
||||||
|
indices.push_back(pairs[k].second);
|
||||||
|
}
|
||||||
|
|
||||||
|
sort(indices.begin(), indices.end());
|
||||||
|
|
||||||
|
for (int k = 0; k < indices.size(); k++) {
|
||||||
|
result[indices[k]] = pairs[i + k].first;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
## day323 2025-01-26
|
||||||
|
### 2127. Maximum Employees to Be Invited to a Meeting
|
||||||
|
A company is organizing a meeting and has a list of n employees, waiting to be invited. They have arranged for a large circular table, capable of seating any number of employees.
|
||||||
|
|
||||||
|
The employees are numbered from 0 to n - 1. Each employee has a favorite person and they will attend the meeting only if they can sit next to their favorite person at the table. The favorite person of an employee is not themself.
|
||||||
|
|
||||||
|
Given a 0-indexed integer array favorite, where favorite[i] denotes the favorite person of the ith employee, return the maximum number of employees that can be invited to the meeting.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题是一道难题,本题有一个很重要的条件即每个人只能喜欢一个人,平时在说到三角恋时常常喜欢用一个图来表示A喜欢B,B喜欢C,C喜欢A,用有向箭头表示每个人喜欢的方向,得到的就是一个三角形仅有三个节点的有向图,那么本题也可以做同样的处理构建出一个有向图。
|
||||||
|
|
||||||
|
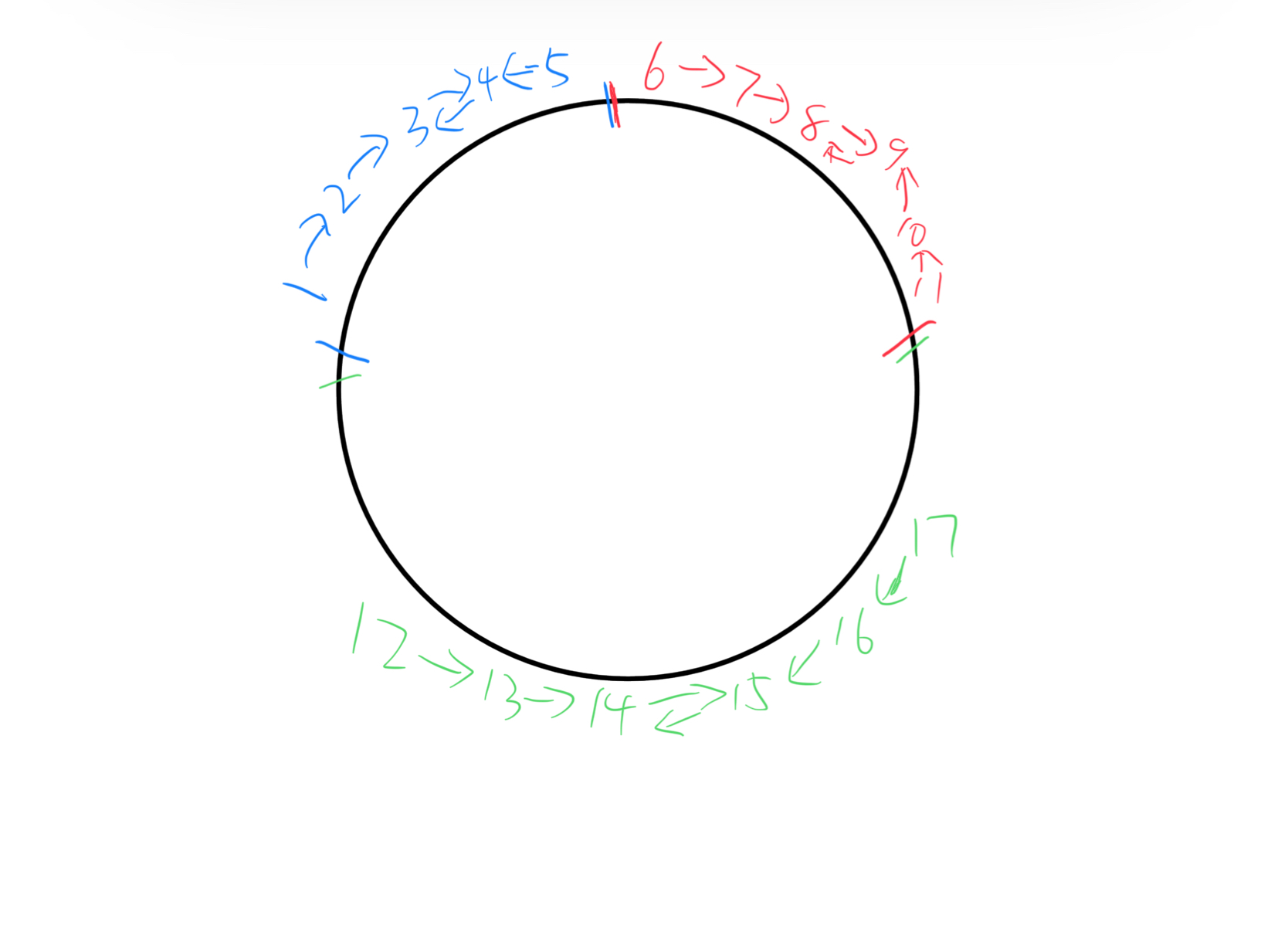
接下来就要考虑这个有向图的特点了,该图任意节点的入度不受限制但出度必定为1。如果我们要让尽可能多的人同时坐在圆桌上,就要找到一条有向图中的路径,这个路径要么自身就是一个环,这样环内的所有人都可以在满足题目条件的情况下坐在同一个圆桌上(类似三角恋,只不过人数更多,从环上任意一点开始最终会回到该点),要么只有一个二元环,即存在一个A喜欢B,B喜欢A的小环,这样只需让A和B坐在一起,再将喜欢A的以及后续一连串人放在A旁边,将喜欢B的及后续一串放在B旁边(如C->D->B)。这样也可以坐在同一个圆桌上且满足题目条件。注意在这一安排的基础上还可以将其他的二元环继续安排在圆桌上,考虑C->D->B,G->E->A的情况,若A和B互相喜欢,则前面提到的两条链可以安排在圆桌上,在C和G之间还可以继续安排其他二元环对应的链(如下方手绘图所示),除此以外均不能安排在同一个圆桌上。那么就要解决找到二元环或者更大的环的问题。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
如何寻找有向图中的环呢,比较经典的是使用拓扑排序,在拓扑排序结束后,如果还有图中的节点没有处理,则说明这些节点位于环中,此时根据环的大小做不同处理,若环大小为2则要将对应的两个节点后面的两条最长的链加和再与之前的二元环得到的双链长度和加和,若环大于2则直接使用环的长度并更新当前的最大环的长度。每个节点后面的最长链的长度可以在拓扑排序的过程中记录下来,当有更长的链时更新链长度即可。最终将双链和与单独的最大环的长度比较取二者中的最大值。
|
||||||
|
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int maximumInvitations(vector<int>& favorite) {
|
||||||
|
int n = favorite.size();
|
||||||
|
vector<int> inDegree(n, 0);
|
||||||
|
vector<bool> visited(n, false);
|
||||||
|
vector<int> dp(n, 1);
|
||||||
|
|
||||||
|
// 计算入度
|
||||||
|
for (int i = 0; i < n; i++) {
|
||||||
|
inDegree[favorite[i]]++;
|
||||||
|
}
|
||||||
|
|
||||||
|
// 拓扑排序的队列
|
||||||
|
queue<int> q;
|
||||||
|
for (int i = 0; i < n; i++) {
|
||||||
|
if (inDegree[i] == 0) {
|
||||||
|
q.push(i);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
// 拓扑排序
|
||||||
|
while (!q.empty()) {
|
||||||
|
int curr = q.front();
|
||||||
|
q.pop();
|
||||||
|
visited[curr] = true;
|
||||||
|
|
||||||
|
int next = favorite[curr];
|
||||||
|
dp[next] = max(dp[next], dp[curr] + 1);
|
||||||
|
inDegree[next]--;
|
||||||
|
if (inDegree[next] == 0) {
|
||||||
|
q.push(next);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
int maxCycle = 0; // 最大环的大小
|
||||||
|
int sumChain = 0; // 所有双向链的和
|
||||||
|
|
||||||
|
// 处理剩余的环
|
||||||
|
for (int i = 0; i < n; i++) {
|
||||||
|
if (!visited[i]) {
|
||||||
|
int cycleLen = 0;
|
||||||
|
int curr = i;
|
||||||
|
// 计算环的大小
|
||||||
|
while (!visited[curr]) {
|
||||||
|
visited[curr] = true;
|
||||||
|
cycleLen++;
|
||||||
|
curr = favorite[curr];
|
||||||
|
}
|
||||||
|
|
||||||
|
// 如果是大小为2的环
|
||||||
|
if (cycleLen == 2) {
|
||||||
|
int len1 = dp[i];
|
||||||
|
int len2 = dp[favorite[i]];
|
||||||
|
sumChain += len1 + len2;
|
||||||
|
} else {
|
||||||
|
maxCycle = max(maxCycle, cycleLen);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
return max(maxCycle, sumChain);
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
## day324 2025-01-27
|
||||||
|
### 1462. Course Schedule IV
|
||||||
|
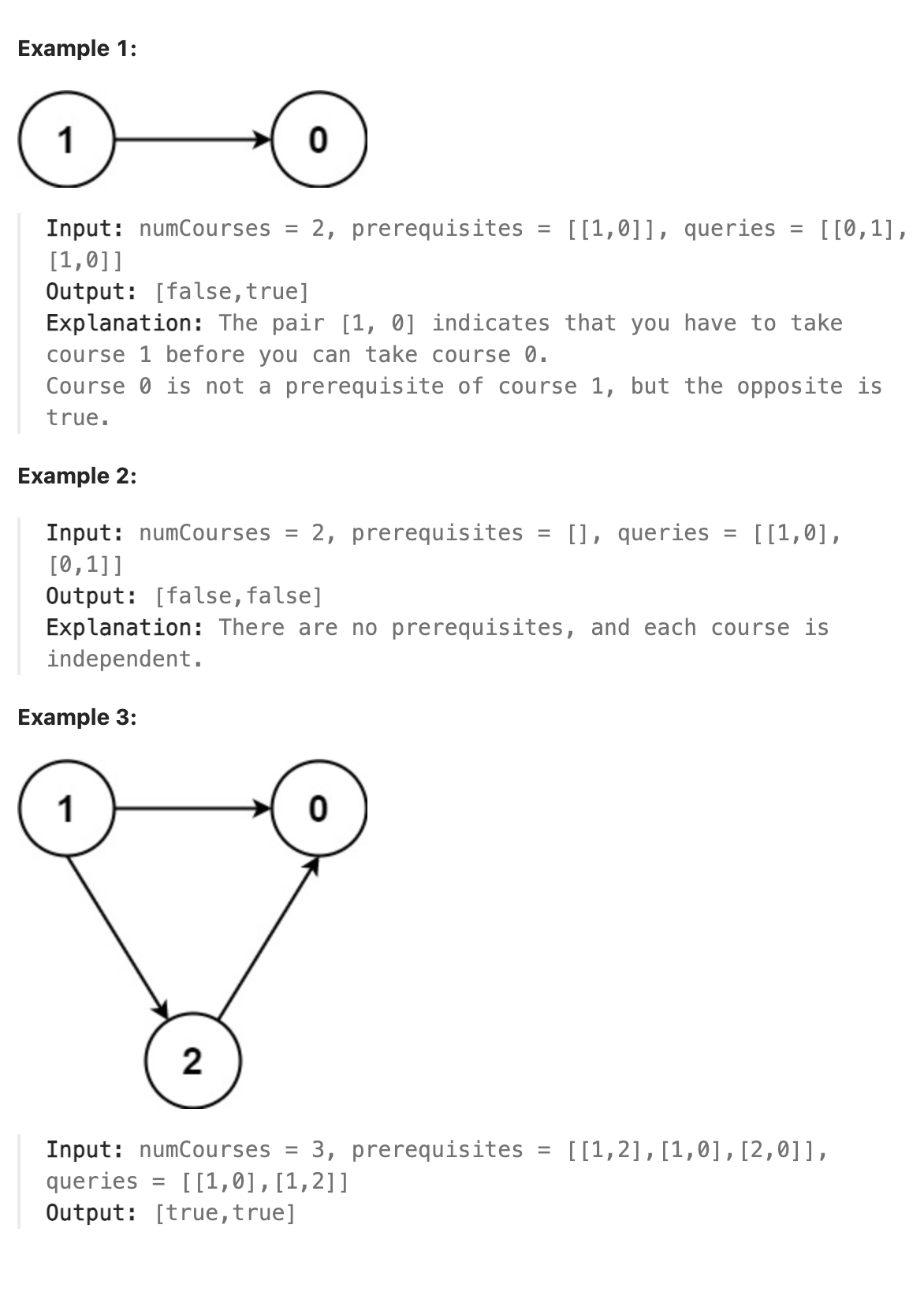
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course ai first if you want to take course bi.
|
||||||
|
|
||||||
|
For example, the pair [0, 1] indicates that you have to take course 0 before you can take course 1.
|
||||||
|
Prerequisites can also be indirect. If course a is a prerequisite of course b, and course b is a prerequisite of course c, then course a is a prerequisite of course c.
|
||||||
|
|
||||||
|
You are also given an array queries where queries[j] = [uj, vj]. For the jth query, you should answer whether course uj is a prerequisite of course vj or not.
|
||||||
|
|
||||||
|
Return a boolean array answer, where answer[j] is the answer to the jth query.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题注意题目中明确说明了题目中不存在环,并且注意到课程数很少(小于等于100)而查询数量可能非常大(10的5次方),因此同样可以先将依赖关系构建成一张图,再遍历所有课程对这些课程既可使用bfs也可使用dfs,此处使用dfs。构建一个二维布尔型数组,数组的行表示前置节点,列下标表示后置节点,数组的值表示前置节点是否是后置节点的前置条件。在搜索过程中将每个节点的后置节点对应的后面的课程传播到当前节点中,即以后置节点为前置条件的节点都会以当前节点为前置条件。考虑到课程数比较小,这样做占用的空间也在可接受的范围内,但会大大加快查询的速度。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int numCourse;
|
||||||
|
vector<bool> checkIfPrerequisite(int numCourses, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
|
||||||
|
numCourse = numCourses;
|
||||||
|
vector<vector<int>> graph(numCourses);
|
||||||
|
for (const auto& prereq : prerequisites) {
|
||||||
|
graph[prereq[0]].push_back(prereq[1]);
|
||||||
|
}
|
||||||
|
|
||||||
|
vector<vector<bool>> isPrerequisite(numCourses, vector<bool>(numCourses, false));
|
||||||
|
|
||||||
|
for (int course = 0; course < numCourses; ++course) {
|
||||||
|
vector<bool> visited(numCourses, false);
|
||||||
|
dfs(course, graph, visited, isPrerequisite);
|
||||||
|
}
|
||||||
|
|
||||||
|
vector<bool> answer;
|
||||||
|
for (const auto& query : queries) {
|
||||||
|
answer.push_back(isPrerequisite[query[0]][query[1]]);
|
||||||
|
}
|
||||||
|
|
||||||
|
return answer;
|
||||||
|
}
|
||||||
|
|
||||||
|
private:
|
||||||
|
void dfs(int course, const vector<vector<int>>& graph, vector<bool>& visited, vector<vector<bool>>& isPrerequisite) {
|
||||||
|
visited[course] = true;
|
||||||
|
for (int nextCourse : graph[course]) {
|
||||||
|
if (!visited[nextCourse]) {
|
||||||
|
isPrerequisite[course][nextCourse] = true;
|
||||||
|
dfs(nextCourse, graph, visited, isPrerequisite);
|
||||||
|
for (int k = 0; k < numCourse; ++k) {
|
||||||
|
if (isPrerequisite[nextCourse][k]) {
|
||||||
|
isPrerequisite[course][k] = true;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
||||||
|
## day325 2025-01-28
|
||||||
|
### 2658. Maximum Number of Fish in a Grid
|
||||||
|
You are given a 0-indexed 2D matrix grid of size m x n, where (r, c) represents:
|
||||||
|
|
||||||
|
A land cell if grid\[r]\[c] = 0, or
|
||||||
|
A water cell containing grid\[r]\[c] fish, if grid\[r]\[c] > 0.
|
||||||
|
A fisher can start at any water cell (r, c) and can do the following operations any number of times:
|
||||||
|
|
||||||
|
Catch all the fish at cell (r, c), or
|
||||||
|
Move to any adjacent water cell.
|
||||||
|
Return the maximum number of fish the fisher can catch if he chooses his starting cell optimally, or 0 if no water cell exists.
|
||||||
|
|
||||||
|
An adjacent cell of the cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) or (r - 1, c) if it exists.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题注意只要相连的有鱼的格子就可以在一次打鱼的过程中全部收走,这就意味着不同的有鱼的区域不会重叠,因为一旦存在重叠就可以在一次打鱼过程中收走,就可以视为同一个区域。这就意味着可以将已经访问过的格子标记为已访问而不会出现同一个格子会被从不同区域重复访问到的情况。则直接从头遍历grid数组,碰到大于0的格子就使用dfs或者bfs,此处使用bfs来向四周遍历,遍历过程中如果遇到大于0的格子就继续遍历,遇到为0的格子就停止遍历,将所有已经访问过大于0的格子都标记为-1,将该区域所有格子中的鱼的个数加和即得该区域的鱼的总和,继续向后遍历grid数组,执行同样的操作。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
int findMaxFish(vector<vector<int>>& grid) {
|
||||||
|
int m = grid.size();
|
||||||
|
int n = grid[0].size();
|
||||||
|
int maxFish = 0;
|
||||||
|
|
||||||
|
vector<pair<int, int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
|
||||||
|
|
||||||
|
for (int i = 0; i < m; i++) {
|
||||||
|
for (int j = 0; j < n; j++) {
|
||||||
|
if (grid[i][j] > 0) {
|
||||||
|
int currentAreaFish = 0;
|
||||||
|
queue<pair<int, int>> q;
|
||||||
|
q.push({i, j});
|
||||||
|
currentAreaFish += grid[i][j];
|
||||||
|
grid[i][j] = -1;
|
||||||
|
|
||||||
|
|
||||||
|
while (!q.empty()) {
|
||||||
|
auto [r, c] = q.front();
|
||||||
|
q.pop();
|
||||||
|
|
||||||
|
for (const auto& dir : dirs) {
|
||||||
|
int newR = r + dir.first;
|
||||||
|
int newC = c + dir.second;
|
||||||
|
|
||||||
|
|
||||||
|
if (newR >= 0 && newR < m && newC >= 0 && newC < n &&
|
||||||
|
grid[newR][newC] > 0) {
|
||||||
|
currentAreaFish += grid[newR][newC];
|
||||||
|
grid[newR][newC] = -1;
|
||||||
|
q.push({newR, newC});
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
maxFish = max(maxFish, currentAreaFish);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
return maxFish;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
## day326 2025-01-29
|
||||||
|
### 684. Redundant Connection
|
||||||
|
In this problem, a tree is an undirected graph that is connected and has no cycles.
|
||||||
|
|
||||||
|
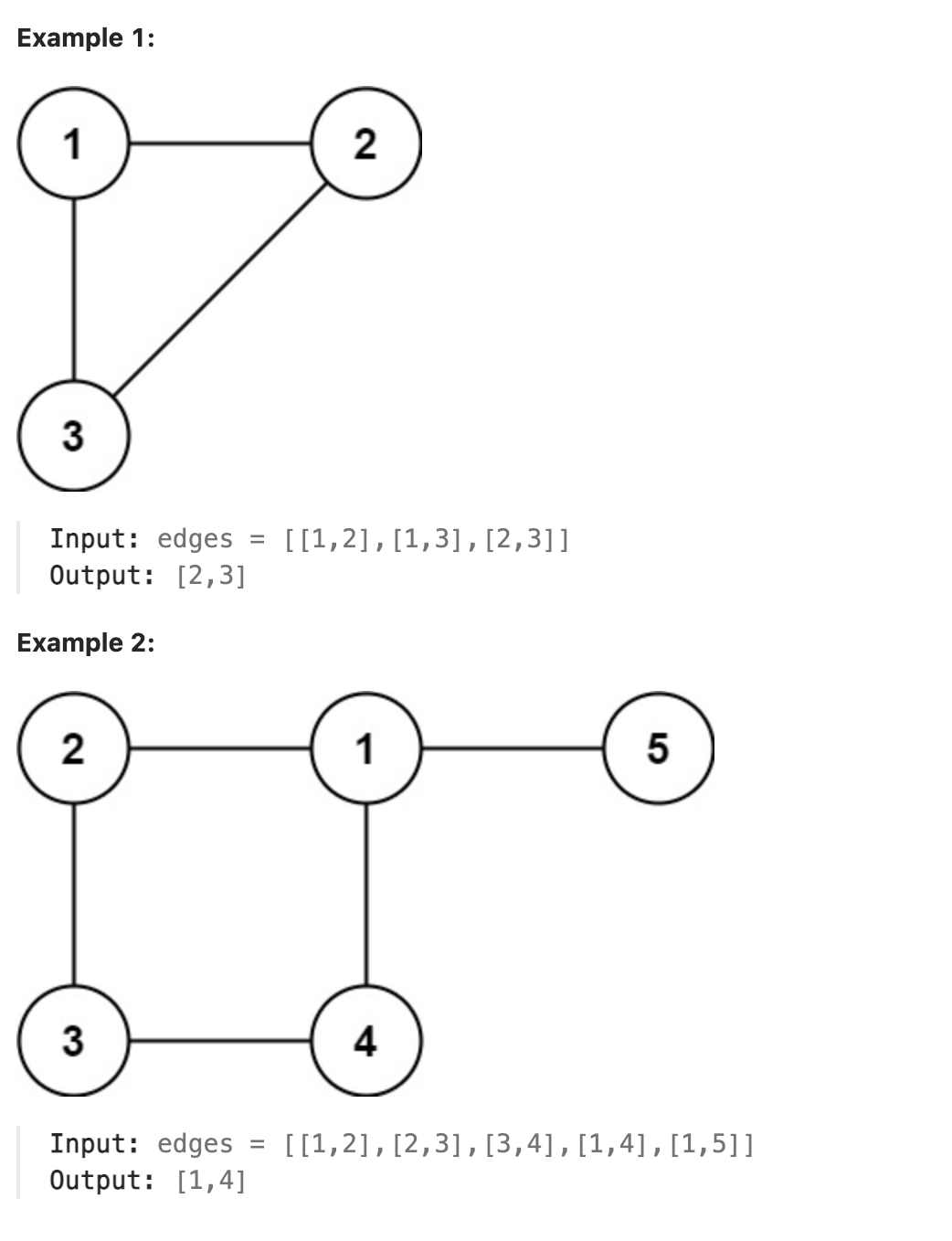
You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.
|
||||||
|
|
||||||
|
Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### 题解
|
||||||
|
本题是一道经典的在无向图中寻找环的问题,比较经典的方法就是使用并查集,依次遍历图中的边,如果两个节点不在同一个集合中就放入同一个集合,如果在同一个集合中则证明到现在为止遍历的全部的边构成的图中存在环且最后遍历的这条边就是环中的一条边,根据题目条件可知图中最多有一个环(只有一个冗余边),则删掉这条边图中就没有环了,剩下的边构成的即为树。而这条边满足输入中最后出现这一条件,因为就是这条边使得图中构成了环。
|
||||||
|
|
||||||
|
### 代码
|
||||||
|
```cpp
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
struct dsu{
|
||||||
|
vector<size_t> pa;
|
||||||
|
explicit dsu(size_t size):pa(size+1){iota(pa.begin(),pa.end(),0);}
|
||||||
|
size_t find(size_t x){
|
||||||
|
while(pa[x]!=x){
|
||||||
|
x = pa[x];
|
||||||
|
}
|
||||||
|
return x;
|
||||||
|
}
|
||||||
|
|
||||||
|
void union_set(size_t x, size_t y){
|
||||||
|
size_t rootX = find(x);
|
||||||
|
size_t rootY = find(y);
|
||||||
|
pa[rootY] = rootX;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
|
||||||
|
dsu unionfind(edges.size());
|
||||||
|
for(const auto& edge : edges){
|
||||||
|
if(unionfind.find(edge[0]) != unionfind.find(edge[1])){
|
||||||
|
unionfind.union_set(edge[0],edge[1]);
|
||||||
|
}else{
|
||||||
|
return edge;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
return vector<int>{};
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|||||||
Reference in New Issue
Block a user