leetcode update

content/posts/leetcode.md

@@ -7680,3 +7680,305 @@ func minDays(bloomDay []int, m int, k int) int {
     return left
 }
 ```
+
+## day115 2024-06-20
+
+### 1552. Magnetic Force Between Two Balls
+
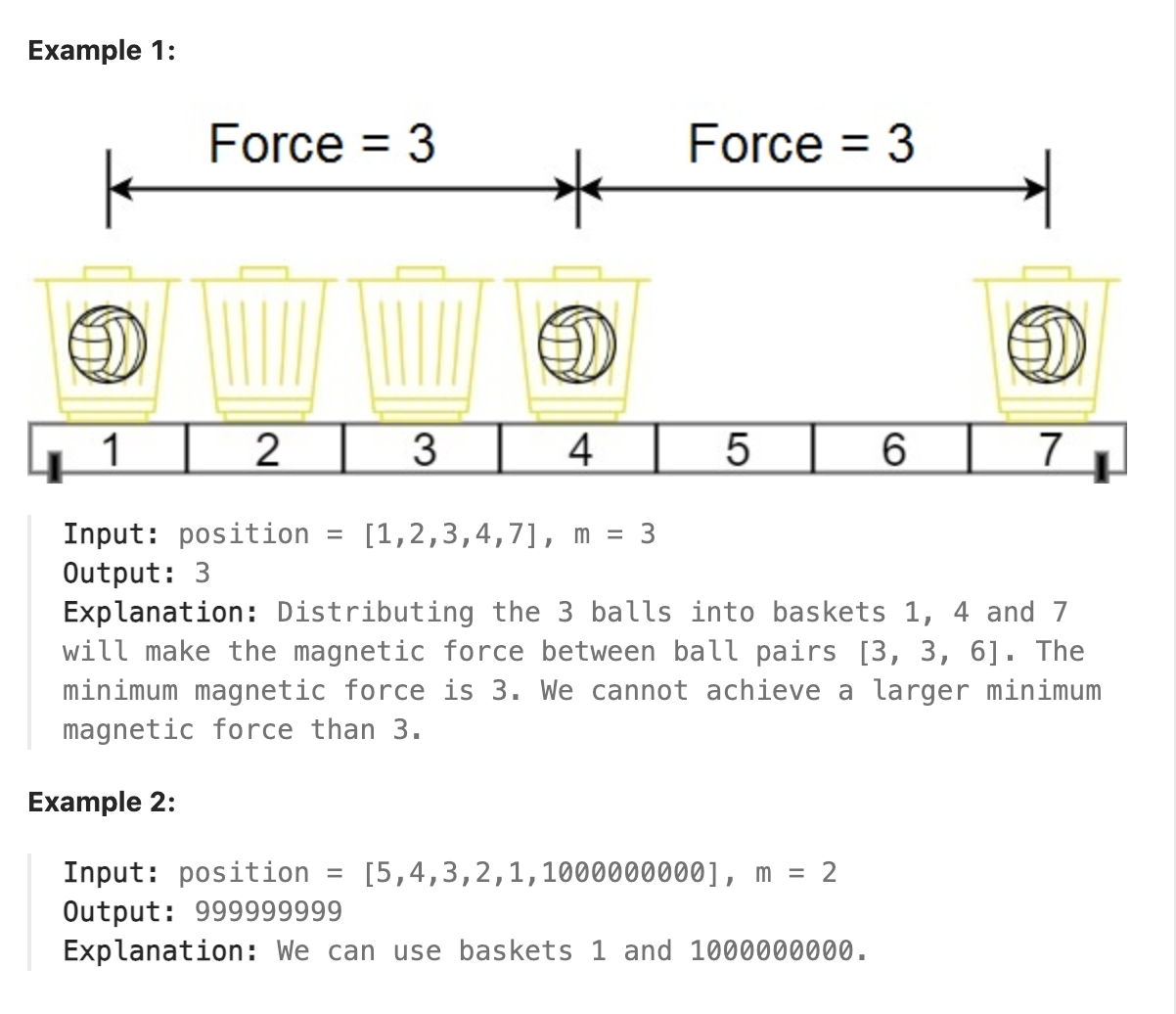
+In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has n empty baskets, the ith basket is at position[i], Morty has m balls and needs to distribute the balls into the baskets such that the minimum magnetic force between any two balls is maximum.
+
+Rick stated that magnetic force between two different balls at positions x and y is |x - y|.
+
+Given the integer array position and the integer m. Return the required force.
+
+![0620ljAJmy7N6uA7](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0620ljAJmy7N6uA7.png)
+
+### 题解
+
+竟然是一道和<瑞克和莫蒂>的联动题(瑞克和莫蒂真的很好看, 强推!!), 要求我们分配这些球, 使得两个球的最小间隔最大. 典型的max-min问题. 解答这种问题因为题目中是要求分配球来获得最终的结果, 使得我们的思路往往起初就会停留在如何分配球这个问题上, 试图通过比较各种分配方式的最小间隔来找到最大的值, 但显然是低效的, 原因在于可能有很多种分配组合都对应着同一个最小间隔. 因此应该转换思路, 给定一个最小间隔, 判断是否有分配方式可以符合这个最小间隔, 只要有一个符合的分配方式, 那么这个最小间隔就是可以取得的, 相当于用这个分配方式代表了所有相同最小间隔的分配方式(代表元思想). 如何判断? 只要在排序后的数组从头到尾遍历, 并采用贪心算法, 和昨天的花束问题类似, 每当间隔大于等于给定的最小间隔就分配一个球, 最后看能分配的球的数量和给定的球的数量之间的相对大小. 大于给定的球则给定最小间隔可以取得. 如何得到最大值? 一样通过二分法, 通过上述判断方法判定中间数值与目标最大值的相对大小, 中间值能取得则将左边界设为中间值, 否则右边界设为中间值. 最终即可得到所求的最大值.
+
+### 代码
+
+```go
+func maxDistance(position []int, m int) int {
+    sort.Ints(position)
+    right := position[len(position)-1]-position[0]
+    left := 1
+
+    for left <= right{
+        mid := (left + right) / 2
+        last := position[0]
+        ballnum := 1
+        dis := 0
+        for _,value := range position[1:]{
+            dis += value - last
+            last = value
+            if dis >= mid{
+                ballnum++
+                if ballnum >= m{
+                    break
+                }
+                dis = 0
+            }
+        }
+        if ballnum >= m{
+            left = mid + 1
+        }else{
+            right = mid - 1
+        }
+    }
+    return right
+}
+```
+
+### 总结
+
+本题和昨天的花束问题有几分相似之处, 体现了一种很重要的思想, 当通过某种组合寻找一由组合产生的属性值, 而多种组合对应同一个属性值时, 可以先假设一个属性值, 再去验证某个组合是否符合. 这样就把问题从求解问题转换为了验证问题. 这里其实和我们平常常用的证明思路正好相反, 平常很多问题证伪只需要举一个反例, 证实则要严格证明,而在今天的问题中, 我们只要找到一个能证实假设的距离成立的组合就足够了, 即证实只要举一个正例即可. 这种题要结合题目的要求, 很多实际生活问题只要能找到一个可行解即可. 这是我们能够用这种方法解题的基础.
+
+很多问题在原问题不容易解决的时候都可以通过一些方式转换成等价的更容易解决的问题, 如计数问题中的自归约问题可将近似求解算法转换成某种采样算法, 通过采样即可得到原问题的近似解(蒙特卡罗)
+
+## day116 2024-06-21
+
+### 1052. Grumpy Bookstore Owner
+
+There is a bookstore owner that has a store open for n minutes. Every minute, some number of customers enter the store. You are given an integer array customers of length n where customers[i] is the number of the customer that enters the store at the start of the ith minute and all those customers leave after the end of that minute.
+
+On some minutes, the bookstore owner is grumpy. You are given a binary array grumpy where grumpy[i] is 1 if the bookstore owner is grumpy during the ith minute, and is 0 otherwise.
+
+When the bookstore owner is grumpy, the customers of that minute are not satisfied, otherwise, they are satisfied.
+
+The bookstore owner knows a secret technique to keep themselves not grumpy for minutes consecutive minutes, but can only use it once.
+
+Return the maximum number of customers that can be satisfied throughout the day.
+
+![0621cuTPeiqgImKT](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0621cuTPeiqgImKT.png)
+
+### 题解
+
+本题中minutes是固定的, 相当于固定长度的minutes可以放置在grumpy数组的任意位置, 将这些位置的数全部变为0, 显然我们需要遍历所有可以放置的位置从而找出能满足的顾客最大值, 因此可以采用滑动窗口从头开始遍历grumpy窗口, 并随着窗口滑动计算当前能满足的顾客数量. 考虑到窗口之外的能满足顾客数量是固定的, 且每次滑动实际上只需要增加窗口后一个的顾客数量且减去窗口最前面的顾客数量, 即可得到每次滑动后能满足的顾客总数. 则初始化先计算出窗口外能满足的顾客总数, 再单独计算窗口内满足的顾客数量. 再将二者加和即得当前能满足的顾客总数. 持续遍历, 按照之前的算法更新能满足的顾客总数并更新最大值.
+
+### 代码
+
+```go
+func maxSatisfied(customers []int, grumpy []int, minutes int) int {
+    outwindow := 0
+    for i,value := range grumpy[minutes:]{
+        if value == 0{
+            outwindow += customers[i+minutes]
+        }
+    }
+    innerwindow := 0
+    for _,value := range customers[:minutes]{
+        innerwindow += value
+    }
+
+
+    maxcus := innerwindow + outwindow
+    temp := maxcus
+    for i,value := range grumpy[:len(grumpy)-minutes]{
+        if value == 1{
+            temp -= customers[i]
+        }
+        if grumpy[i+minutes] == 1{
+            temp += customers[i+minutes]
+        }
+
+        maxcus = max(maxcus, temp)
+    }
+    return maxcus
+}
+```
+
+## day117 2024-06-22
+
+### 1248. Count Number of Nice Subarrays
+
+Given an array of integers nums and an integer k. A continuous subarray is called nice if there are k odd numbers on it.
+
+Return the number of nice sub-arrays.
+
+![0622ujf0vWP4qK3X](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0622ujf0vWP4qK3X.png)
+
+### 题解
+
+这种连续子数组问题是老朋友了, 尤其是这种问符合某个条件的连续子数组个数, 这种题目都采用类似前缀和的思想. 计算从数组开始到当前下标的子数组中奇数的个数, 以奇数个数作为下标, 将从头开始包含这个奇数个数的子数组数目作为数组中的值. 只需要将j下标和j-k下标的数字相乘即可得到从j-k到j包含k个奇数的子数组个数. 从下标k开始遍历"前缀和"数组. 并按照前述方法计算包含k个奇数的子数组个数并加和即可得到最终结果.
+
+### 代码
+
+```go
+func numberOfSubarrays(nums []int, k int) int {
+    state := []int{1}
+    length := 0
+    for _,value := range nums{
+        if value % 2 == 1{
+            length++
+            state = append(state, 1)
+        }else{
+            state[length]++
+        }
+    }
+
+    if length < k{
+        return 0
+    }
+
+
+    result := 0
+    for i, value := range state[k:]{
+        result += value * state[i]
+    }
+    return result
+}
+```
+
+### 总结
+
+其实这种类型的问题核心也是一种转化问题的思路, 即对于求解某一性质为一定值的问题, 可以转化为求解两个区间再做差. 如求解某属性等于k的问题, 可以转化为求解某属性小于等于k和小于等于k-1两个区间后做差的问题. 这种转化适用求解一个区间比求解精准值要容易的多的场景(求解小于等于某个值 往往比求解等于某个值容易得多).
+
+## day118 2024-06-23
+
+### 1438. Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit
+
+Given an array of integers nums and an integer limit, return the size of the longest non-empty subarray such that the absolute difference between any two elements of this subarray is less than or equal to limit.
+
+![0623LJjsHEwXWx9i](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0623LJjsHEwXWx9i.png)
+
+### 题解
+
+本题虽是一道中等难度的题, 但实际比较复杂. 题目很好理解, 需要找到满足子数组内任意两数字差的绝对值小于等于k的所有子数组中最长子数组的长度. 将问题分解开, 首先解决如何确定某个子数组中任意两数字差绝对值是否小于等于k, 只需要知道这个子数组中的最大值和最小值, 二者的差小于等于k则子数组中任意两数字差绝对值都小于等于k. 那么解决这个问题可以使用滑动窗口, 记录当前窗口中的最大值和最小值, 如果满足小于等于k的条件, 则扩大窗口, 判断新加入的数字是否在最小值和最大值的范围内, 在则继续扩大窗口. 否则判断最值更新后当前窗口还能否继续满足小于等于k的条件, 如果不满足则缩小窗口直到满足为止. 满足则继续扩大窗口. 对于某一个特定的子数组, 获知其最小值和最大值比较容易, 遍历一遍数组即可得到. 但使用滑动窗口解题时, 如果每次扩大或者缩小窗口都对窗口内的数字进行遍历显然时间复杂度极高. 我们只需要根据扩大窗口时新增加的数字和缩小窗口时减少的数字来更新最值. 需要解决的问题是, 缩小窗口直到满足条件这一步骤中, 如何判断缩小窗口已经满足条件了呢. 以最小值被更新为例, 如果最小值更新和与当前最大值的差大于k, 则应该缩小窗口直到窗口内的最大值和最小值的差小于等于k. 这意味着, 我们缩小窗口时可能不仅要将窗口缩小到不包含当前最大值, 还可能继续缩小, 直到满足条件为止. 如当前最小值为2, k为3, 而当前窗口中最大值为8, 则我们应缩小窗口直到窗口内最大值小于等于5为止, 这期间我们可能要缩小到不包含8, 再缩小到不包含7, 再缩小到不包含6... 因此我们需要知道数字中大于5的数字都有什么. 这可以用单调队列来解决, 单调减队列保证了后面的数字一定比前面的数字小, 不满足条件的数字都被舍弃. 用一个哈希表保存当前窗口中所有数字和其对应的个数, 缩小窗口时, 减少哈希表中窗口左端数字对应的个数, 直到遇到当前单调队列的队首数字, 同样减少哈希表中的个数, 并判断减少后是否为0, 为0则将其从单调队列中弹出, 否则继续缩小窗口. 直到单调队列队首数字为满足条件的数字. 对于最大值被更新则做类似处理.
+
+因此解答本题我们需要: 1. 哈希表 : 保存当前窗口中各个数字的个数 2. 单调减队列: 保存当前窗口中从最大值开始以及最大值右侧比最大值小且满足单调减顺序的数字(如对于7,5,6 队列中为7,6). 3. 单调增队列 : 保存窗口中从最小值开始及最小值右侧比最小值大且满足单调增顺序的数字(如对于5,7,6 队列中为5,6). 4. 滑动窗口: 解决核心问题
+
+### 代码
+
+```go
+func longestSubarray(nums []int, limit int) int {
+	maxDeque := []int{} // 单调减队列，用来维护最大值
+	minDeque := []int{} // 单调增队列，用来维护最小值
+	left := 0
+	result := 0
+    number := map[int]int{}
+    maxlen := 0
+    minlen := 0
+
+	for right := 0; right < len(nums); right++ {
+        number[nums[right]]++
+		// 维护 maxDeque 为单调减
+		for maxlen != 0 && maxDeque[maxlen-1] <= nums[right] {
+			maxDeque = maxDeque[0:maxlen-1]
+            maxlen--
+		}
+		maxDeque = append(maxDeque, nums[right])
+        maxlen++
+
+		// 维护 minDeque 为单调增
+		for minlen != 0 && minDeque[minlen-1] >= nums[right] {
+			minDeque = minDeque[0:minlen-1]
+            minlen--
+		}
+		minDeque = append(minDeque, nums[right])
+        minlen++
+
+		// 检查当前窗口中的最大值和最小值之差是否超过 limit
+		if maxDeque[0] - minDeque[0] > limit {
+			if nums[right] == minDeque[0]{
+                for maxDeque[0] -  minDeque[0] > limit{
+                    number[nums[left]]--
+                    left++
+                    if number[maxDeque[0]] == 0{
+                        // 最大值出队列
+                        maxDeque = maxDeque[1:]
+                        maxlen--
+                    }
+                }
+            }else if nums[right] == maxDeque[0]{
+                for maxDeque[0] -  minDeque[0] > limit{
+                    number[nums[left]]--
+                    left++
+                    if number[minDeque[0]] == 0{
+                        // 最小值出队列
+                        minDeque = minDeque[1:]
+                        minlen--
+                    }
+                }
+            }
+		}
+
+		// 更新结果
+		if right-left+1 > result {
+			result = right - left + 1
+		}
+	}
+
+	return result
+}
+
+
+```
+
+## 总结
+
+最大值单调队列中的在最大值右侧这一含义为什么如此重要, 因为通过单调队列隐含了一个信息, 即位于当前窗口中单调队列中队列首的数字左侧的数字都比队首数字小, 这一信息使我们可以丢弃一些不必要保存的数字, 因为如果需要缩小窗口, 那么在缩小到这个最大值之前, 窗口中都包含这个最大值, 那么一定不满足要求, 只有在缩小到不包括这个最大值, 才可能满足要求. 这时候再根据单调队列中的数字继续依次判断. 这就是"单调"带来的隐含信息, 这一信息对于简化计算极为重要.
+
+## day119 2024-06-24
+
+### 995. Minimum Number of K Consecutive Bit Flips
+
+You are given a binary array nums and an integer k.
+
+A k-bit flip is choosing a subarray of length k from nums and simultaneously changing every 0 in the subarray to 1, and every 1 in the subarray to 0.
+
+Return the minimum number of k-bit flips required so that there is no 0 in the array. If it is not possible, return -1.
+
+A subarray is a contiguous part of an array.
+
+![0624zB6pKwwpsD6O](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0624zB6pKwwpsD6O.png)
+
+### 题解
+
+本题为一道难题, 要解决最小的翻转次数之前先思考如何判断一个数组能否通过几次翻转最终使得数组内数字全为1, 再考虑如何求得翻转次数的最小值.
+
+如何解决能否通过翻转使得数组内数字全为1的问题呢. 看上去数组中的0可能在任何一个位置出现, 我们也不知道101翻转后的010末尾的0能否和后面的数字组合到一起成为新的一串0. 想让计算机解题也不可能像我们看这个数组一样扫视过去大概估计哪些部分可以翻转, 再通过尝试修正一小部分错误就能得出判断. 计算机不会"估计". 但计算机会"硬算". 因此我们不必如此贪心想一步到位得出答案, 大可以从头开始, 每次只将一个0翻转为1, 遍历到下一个0, 翻转为1, 如此重复每次只将数组中最前面的0翻转为1. 最终如果整个数组都能变成1则该数组可以翻转为全1. 否则不能. 而翻转要相邻的k个位同时翻转, 可用一个固定窗口来表示相邻的k位. 遍历数组, 让窗口内窗口首部的数字为0, 翻转窗口, 将窗口移动到下一个0, 如此重复最终即可判断能否使数组内为全1.
+
+巧合的是, 这种算法同时解决了最小的问题, 即通过这种方式移动窗口并翻转到最后翻转的次数就是最小次数. 原因是最终目标是将数组全部置为1, 因此想实现这个目标, 任何一个0都需要通过翻转变成1, 那么无论哪个位置的0迟早都要被翻转, 意味着任意位置的0对最终结果数量的贡献是均等的, 即时先翻转了后面的0, 前面遗留的0最后还是需要一次翻转, 因此直接从前到后依次翻转就能得到正确答案.
+
+但到这里还没有结束, 这种算法每次都要将整个窗口内的全部数字翻转一遍, 最坏情况下, 窗口每次移动一位, 则总共需要翻转n\*k次. 在k接近n时, 时间复杂度相当于 $n^2$ 级别. 这显然是不可取的, 考虑我们翻转的过程, 如果窗口只向后移动一位, 那么窗口后面的大部分数字经过两次翻转相当于没变. 这提示我们, 没必要真的每次都将每个数字翻转, 只需要记录这个数字被翻转了多少次, 在遍历到这个数字的时候根据翻转次数确定当前数字的值即可. 如何记录某个位置的数字被翻转了多少次? 因为每次翻转都是以一个窗口为单位的, 因此只需记录每次翻转时的窗口尾部到哪里就相当于记录了整个窗口内的数字都被翻转了一次. 用一个单调增数组保存每次翻转窗口尾部的位置, 每次新翻转都将新的尾部放入数组末尾. 对于遍历的每个数字, 将其当前位置和数组首的最小翻转窗口尾部比较, 小于等于这个最小尾部则单调数组的长度就是这个数字被翻转的次数.
+
+### 代码
+
+```go
+func minKBitFlips(nums []int, k int) int {
+    window := 0
+    numlen := len(nums)
+    result := 0
+    fliptail := []int{}
+    for window < numlen{
+        fliplen := len(fliptail)
+        if fliplen != 0{
+            if window <= fliptail[0]{
+                if nums[window] ^ (fliplen % 2) == 0{
+                    fliptail = append(fliptail, window+k-1)
+                    result++
+                }
+            }else{
+                fliptail = fliptail[1:]
+                fliplen--
+                if nums[window] ^ (fliplen % 2) == 0{
+                    fliptail = append(fliptail, window+k-1)
+                    result++
+                }
+            }
+        }else{
+            if nums[window]  == 0{
+                    fliptail = append(fliptail, window+k-1)
+                    result++
+                }
+        }
+        window++
+    }
+    if len(fliptail) == 0 || (len(fliptail) == 1 && fliptail[0] == numlen-1){
+        return result
+    }
+    return -1
+}
+```