leetcode update

content/posts/leetcode.md

@@ -16566,3 +16566,142 @@ private:
 };
 
 ```
+
+## day233 2024-10-27
+
+### 1277. Count Square Submatrices with All Ones
+
+Given a m \* n matrix of ones and zeros, return how many square submatrices have all ones.
+
+![1027QWifWPDPienP](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1027QWifWPDPienP.png)
+
+### 题解
+
+本题对于理解动态规划很有启发意义，数正方形这个任务让我们自己来做，一般会很快的将整个图中的所有大片正方形全部找到，然后依次计算包含的小正方形个数并加和，再计数落单的1并加和。
+
+但这种解法显然是不能落实成算法来实现的，因为我们在“找”图中的所有大片正方形时处理的其实是整个图的全部信息，对图中全部数据都是并行化分析的，是通过一种“形”的思想来寻找这些正方形的。因此我们要考虑，一般而言，对于这样的图，设计算法来解决问题时必然要通过遍历图中数据（无论是按行还是按列）来获取某些信息从而解决问题，但这样的过程存在一个问题，即它不是“并行化”的，而是顺序执行的，这可能有些难理解，我们无论如何遍历数组，终究要从某个起点开始向后一个个遍历，这就意味着必然有一个信息获取的先后顺序，对某一时刻没遍历到的信息我们一无所知，而人脑不一样，我们在看图的时候相当于在一个时刻获取到了图中的全部信息，因此可以做出全局的判断。由此也可以明白为什么卷积要分块处理，其实就是模仿真实的人眼和人脑对图像的信息处理，但其实卷积仍然是一种“伪”并行，因为在每个卷积块内，用计算机来处理时仍然是通过遍历计算进行顺序处理的。
+
+说的有点远，但可以帮助我们理解我们看待问题和通过算法解决问题的视角区别在哪，回归本题，既然用计算机算法无法一次获取“图”中的全部信息，那么至少我们可以通过某种方式将之前已经获取到的图中信息保存起来，这样就不需要再回去查找这些信息，一般而言我们在看待正方形时都会潜意识从左上到右下，因此对于寻找该图中的某个正方形究竟多大，可能也下意识的想固定一个左上的点，再分别向右向下遍历来找出这个正方形最大能有多大，但这样做存在的问题就是右和下都是未遍历过的区域，没有任何信息，因此需要我们自行遍历一遍，而继续移动时可能还要再遍历一些交叉的区域，这些区域有的我们访问过，有的没访问过，这样很难处理。
+
+假如换个角度想想，好好思考下我们遍历这个矩阵的过程，在正常的按行遍历的情况下，我们遍历到的当前位置的左上区域是全部遍历过的，那么如果我们把当前位置看作正方形的右下角，则左上方全部信息都是已知的。想象一下遍历的过程，遍历到任意一个位置时其左上方到（0，0）构成的矩形内所有的点我们都遍历过。那么就可以通过一些保存的信息推知以当前坐标为右下角的正方形的边长最长为多少。
+
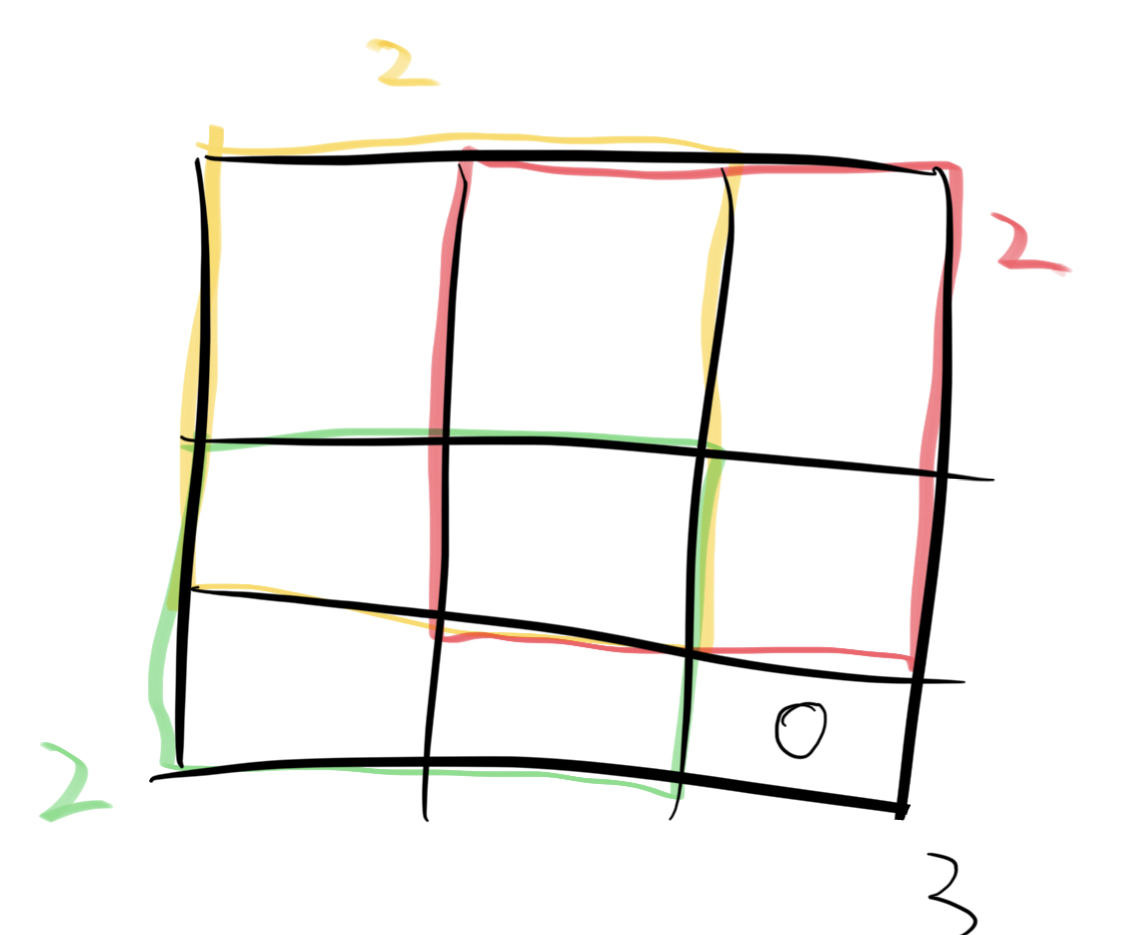
+这时就要用到动态规划了，假设当前位置为(a,b)则若我们知道了(a,b-1)（即按照正常的行遍历时遍历到的前一个位置，因此是比较自然能想到的想法）作为右下坐标的正方形的最大边长，能否知道(a,b)的正方形最大边长。答案是不能，画图简单举个例子即可知道原因。如下所示，可知只有当(a,b-1),(a-1,b),(a-1,b-1)对应的正方形边长均为2时，再增加(a,b)对应的块后正方形边长才能达到3(缺少任意一个小正方形均会导致大正方形缺少某一部分)。则我们取(a,b-1),(a-1,b),(a-1,b-1)中的最小值，这个最小值即为三者对应正方形的最小值，也说明加上(a,b)后可以在该最小值的基础上获得边长大1的更大的正方形，对于正方形的总个数而言就是加上当前更大的正方形边长个数的正方形（如边长为3，则会增加计数边长为1，边长为2，边长为3的以当前坐标为正方形右下坐标的正方形）
+
+![1027SWhMQlIMG_575F593D2E19-1](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1027SWhMQlIMG_575F593D2E19-1.jpeg)
+
+### 代码
+
+```cpp
+class Solution {
+public:
+    int countSquares(vector<vector<int>>& matrix) {
+        int ans = 0;
+        for (int i = 0; i < matrix.size(); i++) {
+            for (int j = 0; j < matrix[0].size(); j++) {
+                if (i && j && matrix[i][j]) {
+                    matrix[i][j] += min({matrix[i - 1][j - 1], matrix[i - 1][j], matrix[i][j - 1]});
+                }
+                ans += matrix[i][j];
+            }
+        }
+        return ans;
+    }
+};
+```
+
+## day234 2024-10-28
+### 2501. Longest Square Streak in an Array 
+You are given an integer array nums. A subsequence of nums is called a square streak if:
+
+The length of the subsequence is at least 2, and
+after sorting the subsequence, each element (except the first element) is the square of the previous number.
+Return the length of the longest square streak in nums, or return -1 if there is no square streak.
+
+A subsequence is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements. 
+
+![10283MKmcTHyw2Ig](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/10283MKmcTHyw2Ig.png)
+
+### 题解
+本题先排序，因为我们要找的其实也是一个有序子序列（后一个数均是前一个数的平方，当然比前面的数字更大），在乱序的情况下很难通过一次遍历找到这样的序列，乱序时可能会遇到一个很大的数还需要后面判断是否有它的因子和以它为因子的数，这样我们要处理更多的可能性，而有序我们只需在遍历时判断是否是以前遇到过的数字的平方。
+
+这里可以使用一个队列用于存放遍历过的数字的平方数和该数字对应的子序列当前的长度，遍历有序数组，判断当前数字是否是队列头部的数字，如果是则将头部弹出并将当前序列长度加1，同时向队列末尾插入当前弹出的数字的平方数。如果当前数字比队列头部数字大则同样弹出队列头部，如果比队列头部数字小则向队列末尾插入当前数字的平方数并将子队列长度设置为1。
+
+### 代码
+```cpp 
+class Solution {
+public:
+    int longestSquareStreak(vector<int>& nums) {
+        struct subseq{
+            long long int val;
+            int leng;
+        };
+        queue<subseq> seq;
+        sort(nums.begin(),nums.end());
+        int maxlen = 1;
+        for (int num : nums){
+            while(!seq.empty() && num>seq.front().val){
+                seq.pop();
+            }
+            if (!seq.empty() && num==seq.front().val){
+                seq.push(subseq{seq.front().val*seq.front().val,seq.front().leng+1});
+                if (seq.front().leng+1 > maxlen){
+                    maxlen = seq.front().leng+1;
+                }
+                seq.pop();
+            }else if(!seq.empty() && num<seq.front().val){
+                seq.push(subseq{long(num)*long(num),1});
+            }else{
+                seq.push(subseq{long(num)*long(num),1});
+            }
+        }
+        return maxlen == 1?-1:maxlen;
+    }
+};
+```
+## day235 2024-10-29
+### 2684. Maximum Number of Moves in a Grid 
+You are given a 0-indexed m x n matrix grid consisting of positive integers.
+
+You can start at any cell in the first column of the matrix, and traverse the grid in the following way:
+
+From a cell (row, col), you can move to any of the cells: (row - 1, col + 1), (row, col + 1) and (row + 1, col + 1) such that the value of the cell you move to, should be strictly bigger than the value of the current cell.
+Return the maximum number of moves that you can perform. 
+
+![1029VHe2DV4tTr5N](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1029VHe2DV4tTr5N.png)
+
+### 题解
+本题每次移动时只能移动到自己后面一列的相邻三个方块内，而且必须移动到比当前方格内数字更大的方格中。则假如我们已知到当前方格的最长移动步数，再根据当前方格相邻方格的数字大小判断能否移动，将当前方格最长移动步数+1与相邻方格之前保存的最长步数比较即可知道相邻的几个方格的最长移动步数。在本题中，通过前一个方格的最长移动步数可以更新后面相邻方格的最长移动步数，因此大问题可以转换为从前一个方格移动到后面相邻方格过程中方格最长移动步数变化的小问题，这些小问题结构均相同。这样就可以通过循环，通过递推最终得到大问题的解。
+
+具体而言，构造一个和矩阵大小相同的dp数组保存到某个方格的最长步数，因为题目限制起始方格只能在第一列，则先遍历第一列方格，找到能移动的相邻方格，并将dp数组中相邻方格位置处的步数设置为1。再遍历第二列，按照同样的方式更新dp数组中第三列的步数值，以此类推，在更新过程中将更新的步数与最大步数比较，不断更新最大步数，最终返回最大步数。
+
+实现过程中要注意一个问题，即在遍历每一列时只有当前那些可以从前一列访问到的格子需要继续向后移动，而那些从前一列中无法访问到的格子是直接忽略的，因为题目要求起点必须从第一列开始，因此从第一列开始移动过程中所有不可达的格子都无需再访问，再访问就会导致从中间某一列的格子开始。同样基于这个原因，遍历过程中可以实现早停，如果某一列中所有格子在从第一列移动到该列时均已经无法访问，则可以结束遍历直接返回结果，因为不会再有**从第一列起始**的更长的路径了。 
+
+### 代码
+```cpp 
+class Solution {
+public:
+    int maxMoves(vector<vector<int>>& grid) {
+        vector<vector<int>> dp(grid.size(), vector<int>(grid[0].size(), -1));
+        int maxmove = 0;
+        for (int i = 0; i < grid.size(); i++) {
+            dp[i][0] = 0;
+        }
+        for (int i=0;i<grid[0].size();i++){
+            bool successmove = false;
+            for (int j=0;j<grid.size();j++){
+                for(int row=-1;row<=1;row++){
+                    if (j+row>=0 && j+row<=grid.size()-1 && i+1<=grid[0].size()-1 && grid[j+row][i+1]>grid[j][i] && dp[j][i]!=-1){
+                        dp[j+row][i+1] = max(dp[j+row][i+1], dp[j][i]+1);
+                        maxmove = max(dp[j+row][i+1], maxmove);
+                        successmove = true;
+                    }
+                } 
+            }
+            if (!successmove){
+                break;
+            }
+        }
+        return maxmove;
+    }
+};
+```