leetcode update

content/posts/leetcode.md

@@ -18335,48 +18335,51 @@ public:
                 start += to_string(num);
             }
         }
-        
+
         vector<vector<int>> neighbors = {
-            {1, 3},    
+            {1, 3},
-            {0, 2, 4}, 
+            {0, 2, 4},
-            {1, 5},    
+            {1, 5},
-            {0, 4},    
+            {0, 4},
-            {3, 1, 5}, 
+            {3, 1, 5},
-            {2, 4}     
+            {2, 4}
         };
-        
+
         queue<pair<string, int>> q;
         unordered_set<string> visited;
-        
+
         q.push({start, 0});
         visited.insert(start);
-        
+
         while (!q.empty()) {
             auto [state, moves] = q.front();
             q.pop();
-            
+
             if (state == target) {
                 return moves;
             }
-            
+
             int zero_pos = state.find('0');
             for (int neighbor : neighbors[zero_pos]) {
                 string new_state = state;
                 swap(new_state[zero_pos], new_state[neighbor]);
-                
+
                 if (visited.find(new_state) == visited.end()) {
                     q.push({new_state, moves + 1});
                     visited.insert(new_state);
                 }
             }
         }
-        
+
         return -1;
     }
 };
 ```
+
 ## day263 2024-11-26
-### 2924. Find Champion II 
+
+### 2924. Find Champion II
+
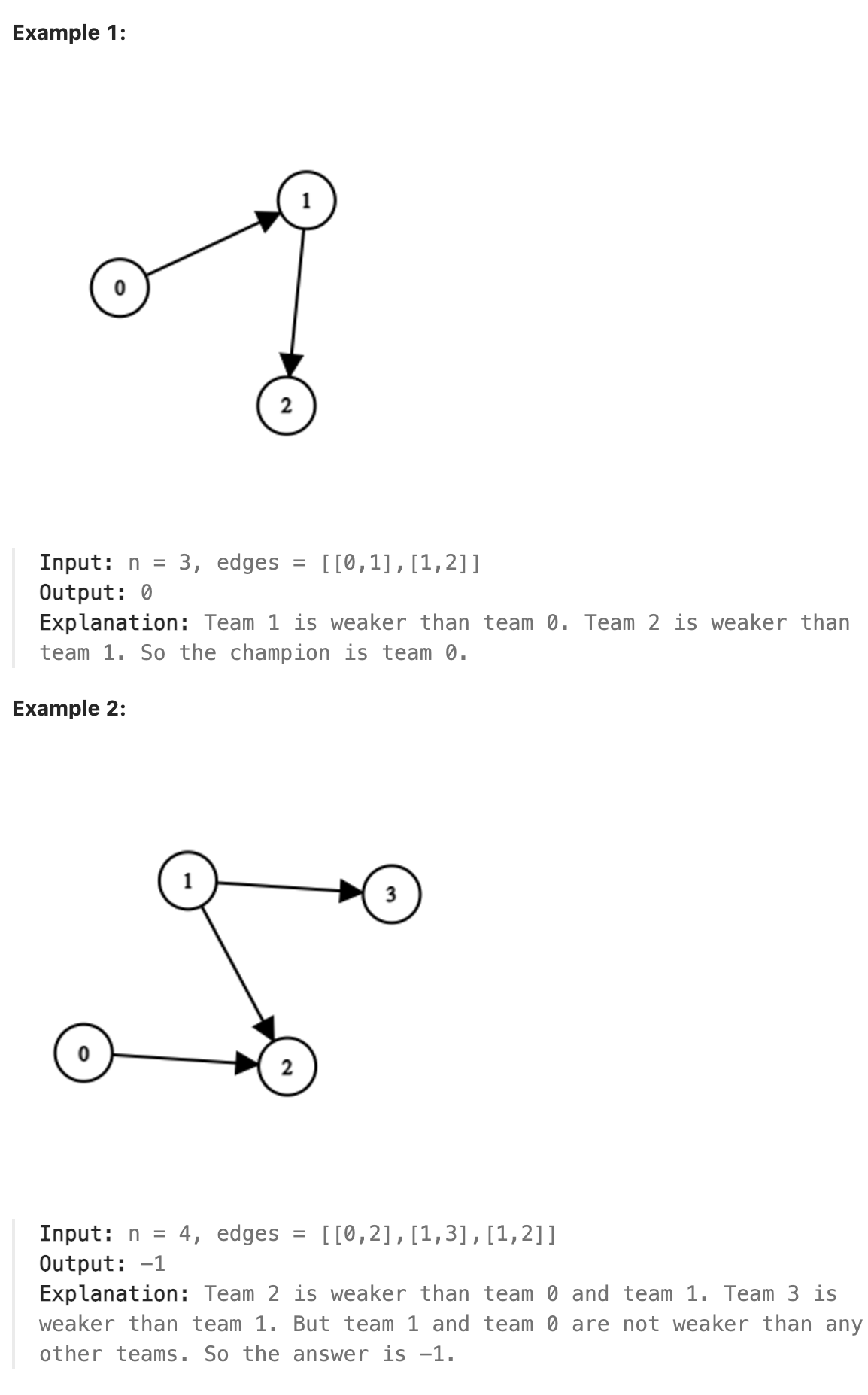
 There are n teams numbered from 0 to n - 1 in a tournament; each team is also a node in a DAG.
 
 You are given the integer n and a 0-indexed 2D integer array edges of length m representing the DAG, where edges[i] = [ui, vi] indicates that there is a directed edge from team ui to team vi in the graph.
@@ -18395,12 +18398,14 @@ A DAG is a directed graph that does not have any cycle.
 ![1126WmfZcBlSPLaH](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1126WmfZcBlSPLaH.png)
 
 ### 题解
+
 本题使用简化版拓扑排序可以解决，拓扑排序在以前的题目中曾经讲解过，在有向无环图中，拓扑排序表示的是一种抽象的先后关系，如若节点均表示数字，则这种先后关系就可以是数字之间的相对大小，若把节点看成一个个在排队的人，则这种先后关系可以是一个人排在另一个人的前面。这种抽象的关系可以对应到各种实际情况中。对于本题，一条有向边相当于一支队伍打赢了另外一支队伍，那么拓扑排序的起始队伍就相当于打赢了其他队伍但没人打赢它，如果这样的队伍只有一个，显然就是冠军，不止有一个那说明还需要更多比赛。
 
 之所以说是简化的拓扑排序，在于本题理解题面可以用拓扑排序的思想，但实际解题，只需要记录下所有节点（队伍）的入度（即有几支队伍打赢了它），最终找到所有入度为0的队伍，只有一个直接返回，否则返回-1。
 
 ### 代码
-```cpp 
+
+```cpp
 class Solution {
 public:
     int findChampion(int n, vector<vector<int>>& edges) {
@@ -18420,8 +18425,11 @@ public:
     }
 };
 ```
+
 ## day264 2024-11-27
-### 3243. Shortest Distance After Road Addition Queries I 
+
+### 3243. Shortest Distance After Road Addition Queries I
+
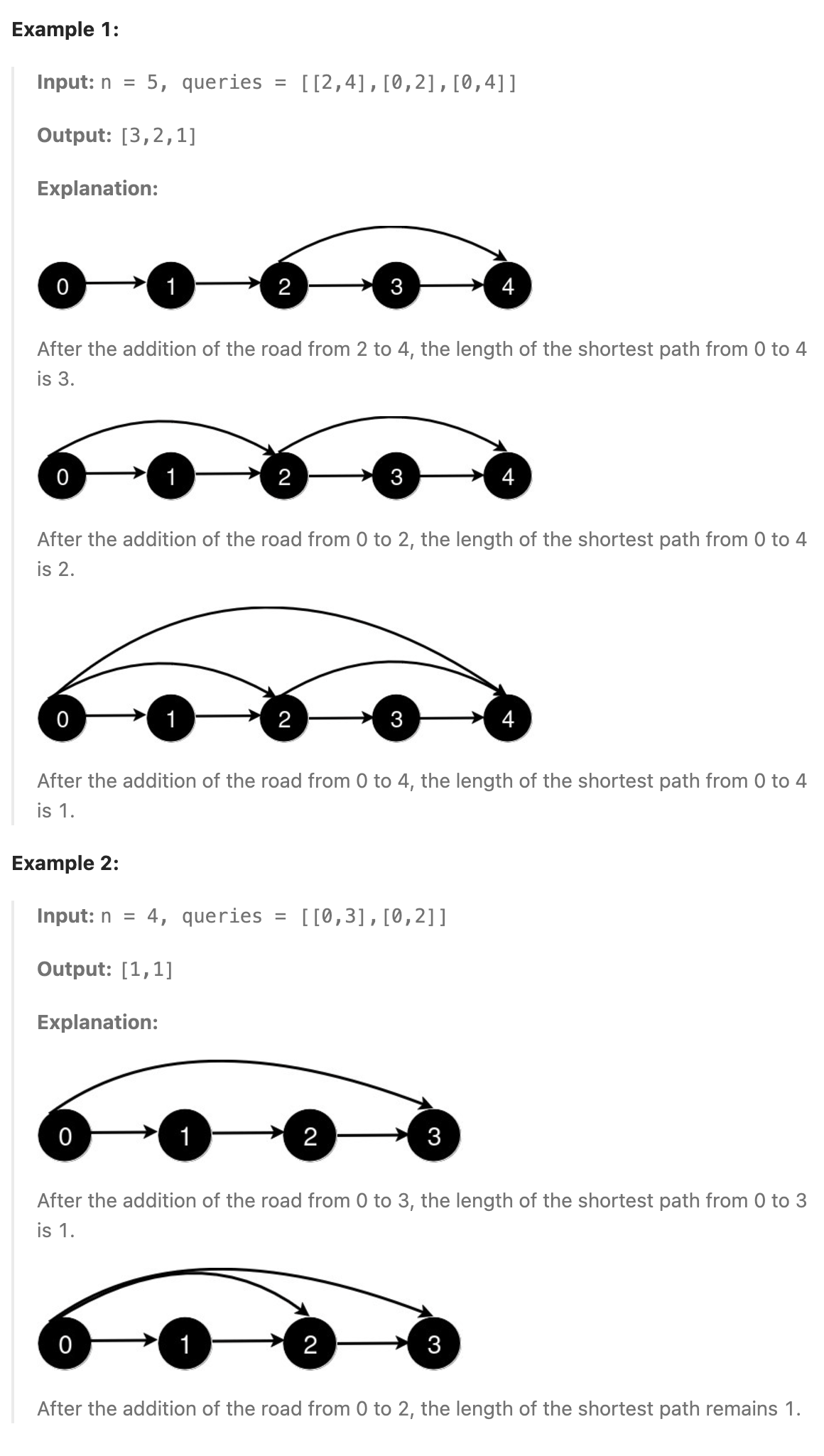
 You are given an integer n and a 2D integer array queries.
 
 There are n cities numbered from 0 to n - 1. Initially, there is a unidirectional road from city i to city i + 1 for all 0 <= i < n - 1.
@@ -18433,53 +18441,55 @@ Return an array answer where for each i in the range [0, queries.length - 1], an
 ![1127SRxWXxnZ7b3M](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1127SRxWXxnZ7b3M.png)
 
 ### 题解
+
 本题每次在增加了一条新路线后可以使用dijistra算法从0节点开始寻找到其他节点的最短路径，一旦找到到n-1节点的最短路径就停止dijistra算法。
 
 最初会想到在添加新路径后可以直接从最初的距离减去添加的新路径中间节省的距离，但这种做法的问题在于新添加的路径可能会与之前添加过的路径有交叉，则无法确定应该减去的节省的距离是多少（如a->b为4,b->c为3，但a->d为5,d->c为1，实际选择d这条路径总距离更短）。而用dijistra算法求出的到每个节点的距离已经是最短距离，一旦确定了到n-1的距离就得到了最终结果。
 
 ### 代码
-```cpp 
+
+```cpp
 
 class Solution {
 public:
     vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
         vector<vector<pair<int, int>>> adj(n);
-        
+
         for(int i = 0; i < n-1; i++) {
-            adj[i].push_back({i+1, 1}); 
+            adj[i].push_back({i+1, 1});
         }
-        
+
         vector<int> answer;
 
         for(const auto& query : queries) {
             int u = query[0];
             int v = query[1];
-            
+
             adj[u].push_back({v, 1});
-            
+
             answer.push_back(dijkstra(adj, n, 0, n-1));
         }
-        
+
         return answer;
     }
-    
+
 private:
     int dijkstra(const vector<vector<pair<int, int>>>& adj, int n, int start, int end) {
         vector<int> dist(n, INT_MAX);
         dist[start] = 0;
-        
+
         priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
         pq.push({0, start});
-        
+
         while(!pq.empty()) {
             int d = pq.top().first;
             int u = pq.top().second;
             pq.pop();
-            
+
             if(u == end) return d;
-            
+
             if(d > dist[u]) continue;
-            
+
             for(const auto& [v, weight] : adj[u]) {
                 if(dist[v] > dist[u] + weight) {
                     dist[v] = dist[u] + weight;
@@ -18487,13 +18497,16 @@ private:
                 }
             }
         }
-        
+
         return dist[end];
     }
 };
 ```
+
 ## day265 2024-11-28
-### 2290. Minimum Obstacle Removal to Reach Corner 
+
+### 2290. Minimum Obstacle Removal to Reach Corner
+
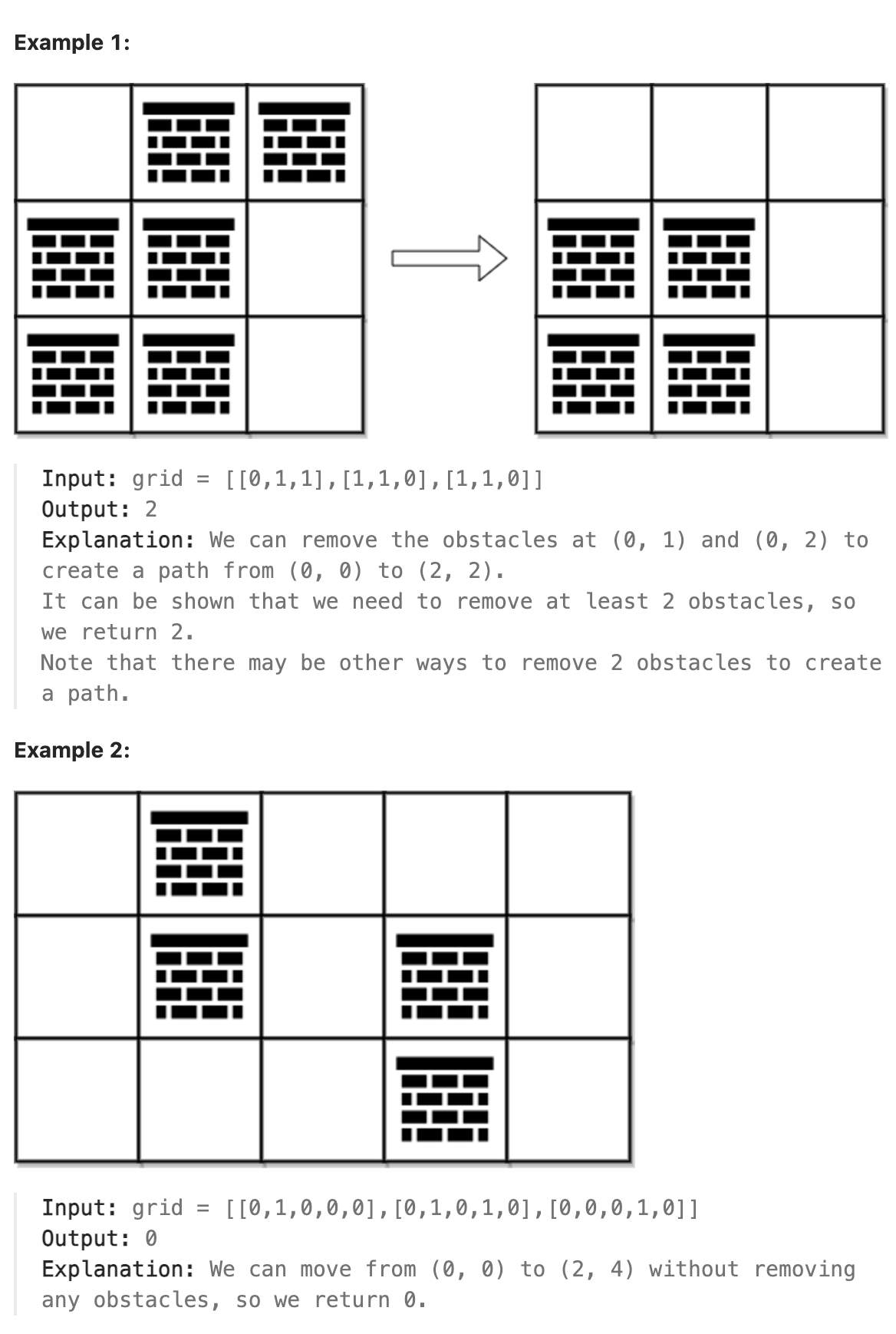
 You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values:
 
 0 represents an empty cell,
@@ -18505,46 +18518,48 @@ Return the minimum number of obstacles to remove so you can move from the upper
 ![11288J5wLzndHQBS](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/11288J5wLzndHQBS.png)
 
 ### 题解
+
 本题是一道难题，关键在于如何建模寻路的过程，一般提到寻路或者路径规划相关的问题，都会想到这是一个图问题，本题中如何将在数组中寻路转换为在图上寻路，并能得到最小成本就是解题的关键。在图上找到成本最小的路径无异于在图上寻找两个节点之间的最短路径，由于边的权重不存在负值，这就是一道典型的可以用dijistra算法解决的问题。
 
 问题在于如何转换，考虑从任何一个位置出发向四个方向移动，如果遇到墙，想要经过墙就必须要花费移除墙的“成本”。最终要求的是移除最少数量的墙的路径，则每个墙都可以视为要花费1点成本。对于没有墙的位置，移动过去不需要花费成本，则将矩阵中每个位置都视为一个独立的节点，如果某个位置有墙，则向这个位置移动的成本就为1，每个位置都和四个方向的其他位置节点之间存在边，如果移动的成本为1，则边权为1，否则为0，此时就转化成了在图上寻找最短路径的问题，可以使用dijistra算法解决。
 
 ### 代码
-```cpp 
+
+```cpp
 
 class Solution {
 public:
     int minimumObstacles(vector<vector<int>>& grid) {
         int m = grid.size();
         int n = grid[0].size();
-        
+
         vector<int> dx = {-1, 1, 0, 0};
         vector<int> dy = {0, 0, -1, 1};
 
         // 优先级队列实现dijistra算法
         priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
-        
+
         vector<vector<int>> dist(m, vector<int>(n, INT_MAX));
-        
+
         dist[0][0] = grid[0][0];
-        pq.push({dist[0][0], 0}); 
+        pq.push({dist[0][0], 0});
-        
+
         while (!pq.empty()) {
             auto [cost, pos] = pq.top();
             pq.pop();
-            
+
             int x = pos / n;
             int y = pos % n;
-            
+
             if (cost > dist[x][y]) continue;
-            
+
             for (int i = 0; i < 4; i++) {
                 int nx = x + dx[i];
                 int ny = y + dy[i];
-                
+
                 if (nx >= 0 && nx < m && ny >= 0 && ny < n) {
                     int newCost = cost + grid[nx][ny];
-                    
+
                     if (newCost < dist[nx][ny]) {
                         dist[nx][ny] = newCost;
                         pq.push({newCost, nx * n + ny});
@@ -18552,14 +18567,16 @@ public:
                 }
             }
         }
-        
+
         return dist[m-1][n-1];
     }
 };
 ```
 
 ## day266 2024-11-29
-### 2577. Minimum Time to Visit a Cell In a Grid 
+
+### 2577. Minimum Time to Visit a Cell In a Grid
+
 You are given a m x n matrix grid consisting of non-negative integers where grid[row][col] represents the minimum time required to be able to visit the cell (row, col), which means you can visit the cell (row, col) only when the time you visit it is greater than or equal to grid[row][col].
 
 You are standing in the top-left cell of the matrix in the 0th second, and you must move to any adjacent cell in the four directions: up, down, left, and right. Each move you make takes 1 second.
@@ -18569,40 +18586,42 @@ Return the minimum time required in which you can visit the bottom-right cell of
 ![1129uNi8EoWpGKuf](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1129uNi8EoWpGKuf.png)
 
 ### 题解
+
 本题仍可以使用dijistra算法解决，像昨天的问题一样，将每个位置视为节点，只不过将每个位置对应的时间视为到这个节点的总成本，同时因为可以在两个节点间来回移动直到时间足够能移动到下一个节点，则只要能从原始位置通过一个时间间隔移动到相邻的位置就可以通过来回移动直到时间足够能移动到下一个相邻可移动位置。但要注意，在来回移动的时候要想继续向当前位置的下一个相邻位置移动，需要移动偶数次步数，因为奇数次步数会移动回当前位置的前一个位置，偶数才会移动回当前位置。
 
 在最开始，只要能从初始位置移动到相邻位置，后面就可以使用dijistra找到到达右下角的最短路径。
 
 ### 代码
-```cpp 
+
+```cpp
 class Solution {
 public:
     int minimumTime(vector<vector<int>>& grid) {
         // 如果一开始就无法移动，直接返回-1
         if (grid[0][1] > 1 && grid[1][0] > 1) return -1;
-        
+
         int m = grid.size(), n = grid[0].size();
         vector<vector<int>> dist(m, vector<int>(n, INT_MAX));
         dist[0][0] = 0;
-        
+
         vector<pair<int, int>> dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
-        
+
-        priority_queue<pair<int, pair<int, int>>, 
+        priority_queue<pair<int, pair<int, int>>,
-                      vector<pair<int, pair<int, int>>>, 
+                      vector<pair<int, pair<int, int>>>,
                       greater<>> pq;
         pq.push({0, {0, 0}});
-        
+
         while (!pq.empty()) {
             auto [time, pos] = pq.top();
             auto [x, y] = pos;
             pq.pop();
-            
+
             if (time > dist[x][y]) continue;
-            
+
             for (const auto& dir : dirs) {
                 int nx = x + dir.first;
                 int ny = y + dir.second;
-                
+
                 if (nx >= 0 && nx < m && ny >= 0 && ny < n) {
                     int nextTime = time + 1;
                     // 需要等待到满足要求的时间
@@ -18613,7 +18632,7 @@ public:
                             nextTime++;
                         }
                     }
-                    
+
                     if (nextTime < dist[nx][ny]) {
                         dist[nx][ny] = nextTime;
                         pq.push({nextTime, {nx, ny}});
@@ -18621,14 +18640,17 @@ public:
                 }
             }
         }
-        
+
         return dist[m-1][n-1] == INT_MAX ? -1 : dist[m-1][n-1];
     }
 };
 
 ```
+
 ## day267 2024-11-30
-### 2097. Valid Arrangement of Pairs 
+
+### 2097. Valid Arrangement of Pairs
+
 You are given a 0-indexed 2D integer array pairs where pairs[i] = [starti, endi]. An arrangement of pairs is valid if for every index i where 1 <= i < pairs.length, we have endi-1 == starti.
 
 Return any valid arrangement of pairs.
@@ -18638,20 +18660,22 @@ Note: The inputs will be generated such that there exists a valid arrangement of
 ![1130P2sjjTCttOLr](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1130P2sjjTCttOLr.png)
 
 ### 题解
+
 本题是一道典型的图问题，每一个pair有一个start和end相当于一个有向边的起始和终止节点。而本题即找图中一条可以一次性经过图中全部边且不重复的路径问题，也就是一个欧拉图问题。这种图问题如果不了解相关知识是比较难解的，像在一个欧拉图中寻找欧拉路径的问题当前已经有比较经典的算法，故本题可以使用Hierholzer算法解决。注意本题中要寻找的是欧拉通路而不是欧拉回路。对于欧拉图的简单介绍可以参考
 
-[欧拉图](https://oi-wiki.org/graph/euler/) 
+[欧拉图](https://oi-wiki.org/graph/euler/)
 
 我们要思考的是，Hierholzer算法是怎么来的，为什么可以想到这样的算法思路。考虑有向图的情况，在有向图中，若图是欧拉图，则起点
 
 ### 代码
-```cpp 
+
+```cpp
 class Solution {
 public:
     vector<vector<int>> validArrangement(vector<vector<int>>& pairs) {
         unordered_map<int, vector<int>> graph;
         unordered_map<int, int> inDegree, outDegree;
-        
+
         for (const auto& pair : pairs) {
             int u = pair[0], v = pair[1];
             graph[u].push_back(v);
@@ -18666,11 +18690,11 @@ public:
                 break;
             }
         }
-        
+
         deque<int> path;
         stack<int> stk;
         stk.push(start);
-        
+
         while (!stk.empty()) {
             int u = stk.top();
             if (graph[u].empty()) {
@@ -18686,27 +18710,31 @@ public:
         for (auto it = path.begin(); it != prev(path.end()); ++it) {
             result.push_back({*it, *next(it)});
         }
-        
+
         return result;
     }
 };
 ```
 
 ## day268 2024-12-01
-### 1346. Check If N and Its Double Exist 
+
+### 1346. Check If N and Its Double Exist
+
 Given an array arr of integers, check if there exist two indices i and j such that :
 
 i != j
 0 <= i, j < arr.length
-arr[i] == 2 * arr[j]
+arr[i] == 2 \* arr[j]
 
 ![1201DFIHsnacqzZu](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1201DFIHsnacqzZu.png)
 
 ### 题解
+
 本题可以使用集合，在遍历数组的过程中将每个数的2倍和1/2都放入集合中，在继续遍历的过程中一旦碰到了集合中已有的数字就返回true，否则返回false。本题只要求返回是否存在这样的组合不要求返回具体的组合对应的下标，故使用集合记录满足条件的数字即能得到最终结果，若要返回具体的下标，则可以构造结构体将每个数对应的原始下标也保存下来。
 
 ### 代码
-```cpp 
+
+```cpp
 class Solution {
 public:
     bool checkIfExist(vector<int>& arr) {
@@ -18724,3 +18752,329 @@ public:
     }
 };
 ```
+
+## day269 2024-12-02
+
+### 1455. Check If a Word Occurs As a Prefix of Any Word in a Sentence
+
+Given a sentence that consists of some words separated by a single space, and a searchWord, check if searchWord is a prefix of any word in sentence.
+
+Return the index of the word in sentence (1-indexed) where searchWord is a prefix of this word. If searchWord is a prefix of more than one word, return the index of the first word (minimum index). If there is no such word return -1.
+
+A prefix of a string s is any leading contiguous substring of s.
+
+![1202hl42cHF424xu](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1202hl42cHF424xu.png)
+
+### 题解
+
+本题将待搜索的单词直接与句子中的单词比较，遇到不同的字符就跳到下一个被空格分隔的单词重新比较，直到遇到能比对成功的单词（计数并返回单词的下标）或者遍历到句子结尾为止。
+
+### 代码
+
+```cpp
+class Solution {
+public:
+    int isPrefixOfWord(string sentence, string searchWord) {
+        int n = searchWord.size();
+        int curindex = 1;
+        int curchar = 0;
+        bool success = true;
+        for (const auto& ch : sentence){
+            if(!success && ch!=' '){
+                continue;
+            }
+            if(ch == ' '){
+                success = true;
+                curchar = 0;
+                curindex++;
+                continue;
+            }
+            if(ch == searchWord[curchar]){
+                curchar++;
+                if(curchar == n){
+                    return curindex;
+                }
+            }else{
+                success = false;
+            }
+
+        }
+        return -1;
+    }
+};
+```
+
+## day270 2024-12-03
+
+### 2109. Adding Spaces to a String
+
+You are given a 0-indexed string s and a 0-indexed integer array spaces that describes the indices in the original string where spaces will be added. Each space should be inserted before the character at the given index.
+
+For example, given s = "EnjoyYourCoffee" and spaces = [5, 9], we place spaces before 'Y' and 'C', which are at indices 5 and 9 respectively. Thus, we obtain "Enjoy Your Coffee".
+Return the modified string after the spaces have been added.
+
+![12032vPuVF4iJOC4](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/12032vPuVF4iJOC4.png)
+
+### 题解
+
+本题按照题意在对应的位置插入空格并构造新字符串，可以创建一个空的新字符串，在扫描原字符串的同时在给定的下标位置插入空格，再继续遍历原字符串，用一个变量记录原字符串遍历到的下标。当遍历到的下标满足要插入空格的位置时在新字符串中插入一个空格，继续遍历并复制原始字符串。
+
+### 代码
+
+```cpp
+class Solution {
+public:
+    string addSpaces(string s, vector<int>& spaces) {
+        string news = "";
+        int index = 0;
+        int n = s.size();
+        for(const int& space : spaces){
+            while(index != space){
+                news.push_back(s[index]);
+                index++;
+            }
+            news.push_back(' ');
+        }
+        news.append(s,index,n);
+        return news;
+    }
+};
+```
+
+## day271 2024-12-04
+
+### 2825. Make String a Subsequence Using Cyclic Increments
+
+You are given two 0-indexed strings str1 and str2.
+
+In an operation, you select a set of indices in str1, and for each index i in the set, increment str1[i] to the next character cyclically. That is 'a' becomes 'b', 'b' becomes 'c', and so on, and 'z' becomes 'a'.
+
+Return true if it is possible to make str2 a subsequence of str1 by performing the operation at most once, and false otherwise.
+
+Note: A subsequence of a string is a new string that is formed from the original string by deleting some (possibly none) of the characters without disturbing the relative positions of the remaining characters.
+
+![1204yOsknB49hUdI](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1204yOsknB49hUdI.png)
+
+### 题解
+
+本题仍是字符串匹配问题，只是做了一些小变动。因为题目中允许我们将指定位置上的字符变换到下一个字符，因此在str1中匹配str2的子序列时，除了和str2中的字符完全相同外，在字母表上比str2的字符小一个位置的字符也可以。
+
+则用指针p遍历str2字符串，并同时用指针q遍历str1字符串直到碰到str2\[p\]和str1\[q\]相同或等于str1\[q\]+1。此时成功匹配str2中的一个字符，移动指针p至下一位，继续用q向后遍历str1重复上述过程，直到将str2完全匹配完返回true或str1已经到末尾但str2仍未完全匹配则返回false。
+
+### 代码
+
+```cpp
+class Solution {
+public:
+    bool canMakeSubsequence(string str1, string str2) {
+        int m = str1.size();
+        const char map[26] = {'z', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y'};
+        int str1index = 0;
+        for (const char& ch : str2){
+            while(ch != str1[str1index] && map[ch-'a'] != str1[str1index]){
+                if(str1index < m){
+                    str1index++;
+                }else{
+                    return false;
+                }
+            }
+            str1index++;
+        }
+        return true;
+    }
+};
+```
+
+## day272 2024-12-05
+
+### 2337. Move Pieces to Obtain a String
+
+You are given two strings start and target, both of length n. Each string consists only of the characters 'L', 'R', and '\_' where:
+
+The characters 'L' and 'R' represent pieces, where a piece 'L' can move to the left only if there is a blank space directly to its left, and a piece 'R' can move to the right only if there is a blank space directly to its right.
+The character '\_' represents a blank space that can be occupied by any of the 'L' or 'R' pieces.
+Return true if it is possible to obtain the string target by moving the pieces of the string start any number of times. Otherwise, return false.
+
+![1205wpH4d2LqKbin](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1205wpH4d2LqKbin.png)
+
+### 题解
+
+本题是一道字符串问题，对于这种问题我们无需考虑将start变为target的具体移动步骤，只需考虑什么条件下一定能通过移动将start中的字符移动为target中的某个字符。对于字符'L'来说，只要target中存在一个'L'在start中这个'L'的相同或者左侧位置并且二者之间的位置全部为空格，就可以将start的'L'移动到target中对应的'L'处，'R'同理。
+
+则可以同时用两个指针分别遍历target和start，每当在target中遇到一个非空字符时，若为'L'则移动start中的指针直到找到一个'L'，若start中的'L'的下标和target中'L'下标相同或者更大（即start中的'L'在target中对应'L'的右侧，这样就可以通过左移移动到target中对应的'L'）。对'R'同理，注意target中L R出现的顺序要与start中相同且start中的非空格字符满足上述的下标条件（'L'在target右侧，'R'在target左侧）。如果全部满足条件则说明可以转换成target，否则不可以。
+
+### 代码
+```cpp 
+class Solution {
+public:
+    bool canChange(string start, string target) {
+        int startindex = 0;
+        int targetindex = 0;
+        int n = start.size();
+        for(targetindex=0;targetindex<n;targetindex++){
+            if (target[targetindex] == '_'){
+                continue;
+            }else if(target[targetindex] == 'L'){
+                while(start[startindex] == '_'){
+                    startindex++;
+                }
+                if (start[startindex] == 'R' || startindex<targetindex || startindex >= n){
+                    return false;
+                }
+                startindex++;
+            }else{
+                while(start[startindex] == '_'){
+                    startindex++;
+                }
+                if (start[startindex] == 'L' || startindex>targetindex || startindex >= n){
+                    return false;
+                }
+                startindex++;
+            }
+        }
+        while(startindex<n){
+            if(start[startindex] != '_'){
+                return false;
+            }
+            startindex++;
+        }
+        return true;
+    }
+};
+```
+## day273 2024-12-06 
+### 2554. Maximum Number of Integers to Choose From a Range I 
+You are given an integer array banned and two integers n and maxSum. You are choosing some number of integers following the below rules:
+
+The chosen integers have to be in the range [1, n].
+Each integer can be chosen at most once.
+The chosen integers should not be in the array banned.
+The sum of the chosen integers should not exceed maxSum.
+Return the maximum number of integers you can choose following the mentioned rules. 
+
+![1206e4MHgtw2CXec](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/1206e4MHgtw2CXec.png)
+
+### 题解
+本题先将banned数组排序，再根据有序的banned数组中的数字和n的范围限制将banned数组中相邻两个数字中间的数字段的全部数字加和，与maxSum比较，小于maxSum则说明这些数字可以全部取得，加到计数总数中，否则使用二分法找到这个数字区间内满足n的范围限制且加和后和小于等于maxSum的最大数字，累加计数即得最终结果。
+
+### 代码
+```cpp 
+
+class Solution {
+public:
+    int maxCount(vector<int>& banned, int n, int maxSum) {
+        sort(banned.begin(), banned.end());
+        
+        vector<int> nums;
+        nums.push_back(0);  
+        for (int x : banned) {
+            if (x <= n) nums.push_back(x);
+        }
+        nums.push_back(n + 1);  
+        
+        int ans = 0;
+        long long sum = 0;
+        
+        for (int i = 1; i < nums.size(); i++) {
+            int left = nums[i-1] + 1;
+            int right = nums[i] - 1;
+            
+            if (left > right || left > n) continue;
+            right = min(right, n);
+            
+            long long count = right - left + 1;
+            long long rangeSum = (left + right) * count / 2;
+            
+            if (sum + rangeSum <= maxSum) {
+                ans += count;
+                sum += rangeSum;
+            } else {
+                int low = left;
+                int high = right;
+                while (low <= high) {
+                    int mid = low + (high - low) / 2;
+                    count = mid - left + 1;
+                    rangeSum = (left + mid) * count / 2;
+                    
+                    if (sum + rangeSum <= maxSum) {
+                        low = mid + 1;
+                    } else {
+                        high = mid - 1;
+                    }
+                }
+                if (high >= left) {
+                    count = high - left + 1;
+                    ans += count;
+                    sum += (left + high) * count / 2;
+                }
+                break;  
+            }
+        }
+        
+        return ans;
+    }
+};
+```
+## day274 2024-12-07
+### 1760. Minimum Limit of Balls in a Bag 
+You are given an integer array nums where the ith bag contains nums[i] balls. You are also given an integer maxOperations.
+
+You can perform the following operation at most maxOperations times:
+
+Take any bag of balls and divide it into two new bags with a positive number of balls.
+For example, a bag of 5 balls can become two new bags of 1 and 4 balls, or two new bags of 2 and 3 balls.
+Your penalty is the maximum number of balls in a bag. You want to minimize your penalty after the operations.
+
+Return the minimum possible penalty after performing the operations. 
+
+![12072UfFSwaDuO8f](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/12072UfFSwaDuO8f.png)
+
+### 题解
+本题起初想到计算出最终能分出的袋子的总数，将球的总数求和再按照尽可能均分的方式将球均分到袋子中，但这种思路在本题并不适用，因为均分后的最少的球的个数可能比当前某些袋子中已有的球的个数要多，而题目只允许将袋子中的球分开而不允许向袋子中添加球，因此这种情况是不符合题目要求的。我们只能通过模拟拆分的方式来模拟球的拆分过程最终得到每个袋子中球的个数。
+
+既然只能通过模拟拆分方式来得到最终每个袋子中球的分配，那么必须要对拆分过程进行一个限制，这里我们可以限制允许拆分出来的每个袋子中球的最大个数，可以从具有最多球的袋子中球的个数减一开始，依次减一作为最大个数限制并模拟拆分过程来判断最终能否在满足我们自己定义的限制条件下拆分成功。如果成功，则可继续减小限制，不成功则不能继续减小限制。
+
+一个一个的减少个数限制效率比较低，此时发现其实“能否在最大个数限制下成功拆分”是一个二元条件，具有一个临界值，即比该临界个数大的个数限制必定都可以成功拆分，而小于该临界个数的个数限制必定不能成功拆分。因此可以使用二分法找到这个临界限制，这个临界限制就是我们最终要求的最小可能惩罚。
+
+### 代码
+```cpp 
+
+class Solution {
+public:
+    // 检查在给定的最大球数限制下是否可以完成分割
+    bool canSplit(vector<int>& nums, int maxOperations, int limit) {
+        int operations = 0;
+        for (int num : nums) {
+            operations += (num - 1) / limit;
+            if (operations > maxOperations) {
+                return false;
+            }
+        }
+        return true;
+    }
+    
+    int minimumSize(vector<int>& nums, int maxOperations) {
+        int maxNum = 0;
+        for (int num : nums) {
+            maxNum = max(maxNum, num);
+        }
+        
+        int left = 1;
+        int right = maxNum;
+        int result = maxNum;
+        
+        while (left <= right) {
+            int mid = left + (right - left) / 2;
+            
+            if (canSplit(nums, maxOperations, mid)) {
+                result = mid;
+                right = mid - 1;
+            } else {
+                left = mid + 1;
+            }
+        }
+        
+        return result;
+    }
+};
+```