leetcode update

2025-04-20 05:52:07 +08:00 · 2024-09-23 15:20:37 +08:00 · 2024-09-23 15:20:37 +08:00 · 0149d9ca67
commit 0149d9ca67
parent 8bedd7a0ac
1 changed files with 175 additions and 0 deletions
--- a/content/posts/leetcode.md
+++ b/content/posts/leetcode.md
@ -13724,3 +13724,178 @@ public:
    }
 };
 ```
 ## day208 2024-09-22
 ### 440. K-th Smallest in Lexicographical Order
 Given two integers n and k, return the kth lexicographically smallest integer in the range [1, n].
 ![0922rJ3xhbTWPf0e](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0922rJ3xhbTWPf0e.png)
 ### 题解
 本题是一道难题。
 我们有昨天题目的基础，可能会觉得只需在昨天题目解法的基础上返回数组中的第k个数。实际操作中可以发现会出现MLE和TLE的问题。显然不是这么简单扩展一下就能解决的问题，先考虑MLE的问题，考虑到最终我们只需要返回第k大的数字，则没必要用result数组来保存所有数字，只需在遍历到第k大的数字时将结果赋给变量并退出递归函数，这样只需要一个变量保存最终结果，避免了n过大时MLE的问题。再考虑TLE的问题，因为本题中n和k的取值范围都非常大，我们需要想一些方法来对字典序的数字的生成树进行计数，通过计数直接定位到每个位上的数字是什么。
 我们需根据树的节点个数不断一层层判断当前层应当选择哪个节点直到最低层，被选择过的层之上的节点个数应从目标中减去，因为这些节点都是有意义的，表示比较短的数字（如两层的情况，根节点表示1这个数字，这个数字本身也是序列中的一部分）。并将选择的节点对应的数字连接即得最终的结果。（也可理解为根据子树的节点个数选择需要遍历的节点，记录遍历路径即得最终结果，算是一种启发式遍历）。
 在每一层中，根据已经遍历过的节点前缀计算0节点对应的子树节点个数，将节点个数与当前总节点个数加和并与目标k比较，小于等于k则继续计算下一个相邻节点对应的子树节点数，如此反复直到找到目标k所属的节点子树。则该节点的值为下一位的值，继续遍历该节点对应的子树的下一层按照上面的方式寻找下一层中目标k对应的节点。注意每棵树的节点个数是受到n限制的，即该树的所有路径得到的数字均需小于等于n。
 如何对某个已知前缀的子树中的节点个数进行计数呢？先判断当前前缀pre1是否小于等于n，再比较(pre1+1)(pre2)和n的大小，如果pre2比n小，说明该层是满的，此时应该给计数加上当前层的节点个数，即从根节点开始1，10...10^k(k表示层数)。给pre1和pre2均乘10进入树的下一层再继续判断下一层是否是满的，这里可以发现由于一开始pre2=pre1+1，则实际上若某一层的节点是满的，该层的节点个数就是pre2-pre1(和10^k相等)。如果节点不是满的，那么该层节点个数是n-pre1（注意这个过程中pre1一直是变化的，不断乘10）。举例来说，假如当前前缀为12，n为140，则以该前缀作为根节点的子树节点个数为13-12+(13\*10-12\*10)=11。假如当前前缀为12，n为125则节点个数为(13-12)+(125-12\*10)，因为125<13\*10=130。再结合下面的图理解。
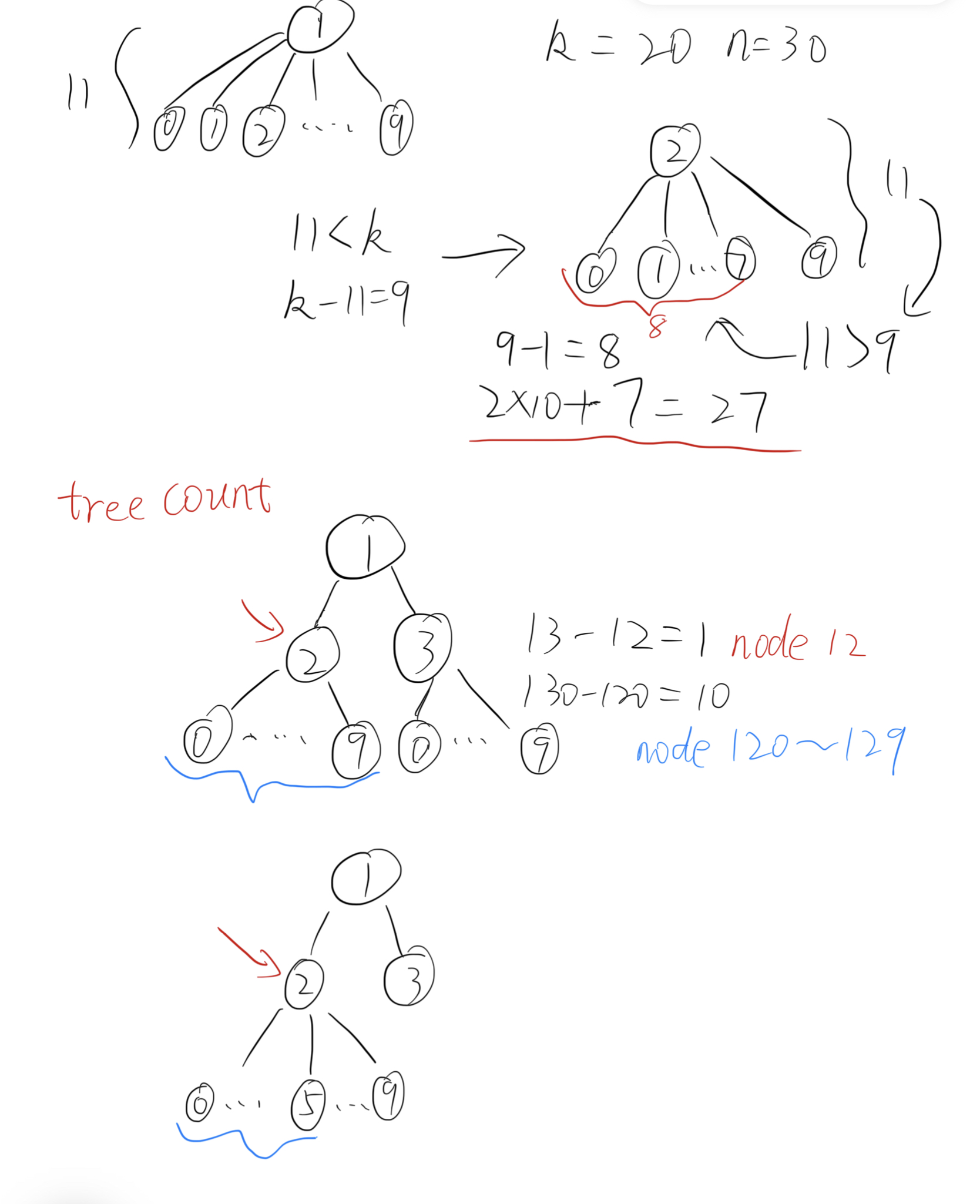
 ![0922mnOFiWIMG_E0C343C9BCC8-1](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0922mnOFiWIMG_E0C343C9BCC8-1.jpeg)
 为什么采用昨天的解法会超时而这种解法就快得多，在这种解法中，通过不断计数子树的节点数来选择某一层对应的节点相当于一位一位的确定最终数字的某一位，相当于一种“十分法”。“二分法”是通过目标值和当前中间值的相对大小确定属于左右哪个区间，这里的“十分法”类似，通过比较目标k和当前10个区间的前n个区间的节点总数大相对大小确定目标k属于哪个区间。再继续将这个小区间作为整体再次10分。直到找到目标数字。
 ### 代码
 ```cpp
 class Solution {
 public:
    int findKthNumber(int n, int k) {
        int curr = 1;
        k--;
        while (k > 0) {
            long long steps = countSteps(n, curr, curr + 1);
            if (steps <= k) {
                k -= steps;
                curr++;
            } else {
                k--;
                curr *= 10;
            }
        }
        return curr;
    }
 private:
    long long countSteps(long long n, long long n1, long long n2) {
        long long steps = 0;
        while (n1 <= n) {
            steps += min(n + 1, n2) - n1;
            n1 *= 10;
            n2 *= 10;
        }
        return steps;
    }
 };
 ```
 ## day209 2024-09-23
 ### 2707. Extra Characters in a String
 You are given a 0-indexed string s and a dictionary of words dictionary. You have to break s into one or more non-overlapping substrings such that each substring is present in dictionary. There may be some extra characters in s which are not present in any of the substrings.
 Return the minimum number of extra characters left over if you break up s optimally.
 ![0923oan93ei5Pq70](https://testingcf.jsdelivr.net/gh/game-loader/picbase@master/uPic/0923oan93ei5Pq70.png)
 ### 题解
 本题考虑字符串任何一个位置之前的子字符串中的最小extra字符个数可以如何求得，则如果把该位置i自己当作一个extra字符，那么其之前的最小extra字符个数即为extra\[i-1\]+1。如果位置i对应的字符是某个字典中某个字符串的末尾，设这个字符串长度为k，则extra\[i\]=extra\[i-k\]。注意i可能是多个字符串的末尾，则我们取这些这些字符串计算得到的所有extra\[i\]和extra\[i-1\]+1中的最小值。
 我们可以从后向前遍历字符串s，按照上面的解法通过不断递归求得当前位置的extra\[i\]。这是大多数题解中的做法，但一般而言我们先想到的还是从前向后遍历字符串，如何在从前向后遍历时求得各个位置的extra\[i\]呢。我们考虑任意位置i，假设该位置的extra\[i\]是已知的。则若我们找到所有以位置i字符开头的包含在字典中的字符串，设该字符串末尾的位置为j，则extra\[j\]=min(extra\[i\],extra\[j\])。那么可以找到所有这样的字符串并更新对应位置的extra。当遍历到j位置时，再将j位置的字符当作extra字符，比较extra\[j-1\]+1和extra\[j\]的大小并取较小值。这样假如存在位置i和位置k，以这两个位置开头的字符串都存在于字典中且均以位置j结尾，则当遍历完i和k时，j位置的extra\[j\]的值就会是min(extra\[i\],extra\[k\])。以此类推可知最终extra\[j\]一定能取到最小值（表示j之前的子字符串中的最少extra字符个数）。
 这里我们寻找所有以位置i的字符开头的在字典中的字符串时，如果有多个字符串均符合，则短的字符串必定为长的字符串的前缀串（因为字符串s是固定的，判断字符串是否在字典中是不断遍历s得到的）。判断某个字符串是否在一个字符串集合中，字典树Trie是常用的快速判断方法，而在本题中使用trie的优势在于相同前缀的字符串无需再从头开始比较字符，直接沿着之前前缀串的最后一个节点继续向下查找即可，大大加快了查找速度。
 ### 代码
 ```cpp
 const int ALPHABET_SIZE = 26;
 struct TrieNode {
    TrieNode* children[ALPHABET_SIZE];
    bool isEndOfWord;
    TrieNode() : isEndOfWord(false) {
        for(int i = 0; i < ALPHABET_SIZE; ++i){
            children[i] = nullptr;
        }
    }
 };
 class Trie {
 public:
    TrieNode* root;
    Trie() { root = new TrieNode(); }
    void insert(const string &word) {
        TrieNode* node = root;
        for(char c : word){
            int index = c - 'a';
            if(index < 0 || index >= ALPHABET_SIZE){
                continue;
            }
            if(node->children[index] == nullptr){
                node->children[index] = new TrieNode();
            }
            node = node->children[index];
        }
        node->isEndOfWord = true;
    }
    ~Trie() {
        function<void(TrieNode*)> deleteTrie = [&](TrieNode* node) {
            if(node == nullptr) return;
            for(int i = 0; i < ALPHABET_SIZE; ++i){
                if(node->children[i] != nullptr){
                    deleteTrie(node->children[i]);
                }
            }
            delete node;
        };
        deleteTrie(root);
    }
 };
 class Solution {
 public:
    int minExtraChar(string s, vector<string>& dictionary) {
        int n = s.size();
        Trie trie;
        for(const string &word : dictionary){
            trie.insert(word);
        }
        vector<int> dp(n + 1, INT32_MAX);
        dp[0] = 0;
        for(int i = 0; i < n; ++i){
            if(dp[i] + 1 < dp[i+1]){
                dp[i+1] = dp[i] +1;
            }
            TrieNode* node = trie.root;
            int j = i;
            while(j < n){
                int index = s[j] - 'a';
                if(index < 0 || index >= ALPHABET_SIZE || node->children[index] == nullptr){
                    break;
                }
                node = node->children[index];
                ++j;
                if(node->isEndOfWord){
                    if(dp[i] < dp[j]){
                        dp[j] = dp[i];
                    }
                }
            }
        }
        return dp[n];
    }
 };
 ```